Comment capturer la forme de nos données ? Ont-elles une « apparence » ?
Dans les deux précédents articles (1, 2), j’avais émis en marge des remarques et des hypothèses sur la nature « métrique » des matrices de similarité parfaites. J’ai également mentionné la distance de Wasserstein dont je n’ai pas fait grand chose étant donné la difficulté d’en extraire une métrique. Cela m’a convaincu d’aller voir ce qu’il se faisait du côté de la topologie appliquée au traitement des données. Dans cet article, j’exposerai une approche parallèle pour évaluer la qualité des données produites par un LLM pour des tâches de type indexation : il s’agira de regarder leur « forme ». Cette approche topologique des données, sans être un outil miraculeux, pourrait être complémentaire en contexte patrimonial ou documentaire pour l’analyse des données.Notez que je suis encore en phase de digestion de ce que j’ai découvert du côté de la TDA (Topological Data Analysis) donc il y a probablement des maladresses. Tout ce qui est présenté ici est voué à être développé (dans l’idéal), et notamment autour de la problématique du diagnostic des tâches de normalisation de données documentaires. J’avais besoin de poser ce jalon — ce petit topo de mes préoccupations du jour– pour guider mes réflexions futures. Si les mathématiques derrière ne sont pas vraiment triviales (ou du moins exigent de prendre le « pli » topologique), j’ai essayé de capturer et de partager quelques intuitions et idées conquises par sympathie.
Dans le fond, quand on compare une vérité terrain et des données générées, il s’agit de comparer leurs formes respectives. Quand la vérité terrain représente une configuration réputée parfaite, une référence utile pour établir et quantifier des différences, les données générées, elles, en sont une reprise bruitée, érodée — chaîne de traitement oblige. A chaque étape (OCRisation, prompt, modèles de données Pydantic, génération…) on risque de perdre de l’information. Se pose alors une question presque philosophique, pouvant presque nous ramener du côté d’Henri Bergson ou de René Thom : qu’est-ce qui persiste entre la vérité terrain et les données prédites ? S’il semble bien qu’il y ait une persistance de l’information, malgré les pertes, cela veut dire qu’il y a une « forme », reconnaissable malgré le changement ? Comment « s’individuent » les données ?

La pipeline d’évaluation décrite dans les articles précédents reposait sur le transport optimal : deux éléments d’ensembles distincts très similaires peuvent être appariés au regard de leur proximité (distance de Levenstein ou Ratcliff/Obershelp). Sans revenir en détail sur ce que j’ai déjà écrit, j’ai calculé en amont une matrice de coût pour préparer cet appariement et, avec des métriques appropriées, en évaluer la qualité. Cette problématique d’optimisation était un préalable. Elle impliquait de penser à de nouvelles métriques pour évaluer la qualité des données prédites modulo la qualité des appariements eux-mêmes. Il n’était donc pas question de comparer les formes des données dans leur ensemble, mais bien d’évaluer au niveau des paires leur qualité. Ici, le score global vient du bas et remonte : c’est l’ensemble des qualités « locales » qui déterminent, par touches discrètes, le paysage qualitatif.

On a bien sûr usé de stratagèmes qui prennent en compte de la structure globale des données pour évaluer la robustesse des matches (avec une intégrale qui calcule le nombre d’appariements sur un seuil balayé). Mais on part du « grain » des données pour tenter d’en remonter la qualité globale, de la même façon qu’on peut remontrer le bruit de la mer depuis la percussion des gouttes. On a établi des métriques « ascendantes » qui partent des différences pour faire remonter la surface des qualités. Nos appariements se comportaient comme des monades : mais si on leur ajoutait portes et fenêtres pour qu’elles puissent lier des relations jusqu’à faire monter une forme ou un motif ?
Le transport optimal reste pertinent car ça permet bien de relier, dans notre cas, deux informations à appareiller malgré le désordre que peut semer le LLMs, malgré la sortie structurée.
Alors arrive cette question fertile : et si on donnait une forme à nos deux ensembles de données (vérité terrain / données prédites) et qu’on les comparait ? Et si on pouvait, depuis la forme globale, proposer une métrique plus « descendante »? Peut-on dégager des indicateurs plus « formels » ? Il y aurait de quoi picorer dans la mangeoire topologique.
Le but ici est d’expérimenter avec des données que l’on connaît bien qu’on peut réutiliser pour prendre en main la TDA. Donc on récupère nos données prédites et vérité terrain du travail de la dernière fois. Evidemment, le potentiel de la TDA ne sera pas ici à son paroxysme, mais on pourra imaginer, j’espère, le potentiel de la méthode avec des approches sémantiques (embeddings).
Donner une forme aux données : de l’appariement local à la comparaison globale
État des lieux
Comparer deux ensembles de points, c’est bien et ça fonctionne de façon satisfaisante. Mais cela reste une approche locale — on cherche à associer un point de vérité terrain à un point prédit. Or, la structure spatiale, la « forme » globale de ces points, contient souvent une richesse d’information précieuse qui peut compléter l’analyse des appariements ponctuels. On pourrait compléter le point de vue ascendant en regarder l’aspect global des données.
L’idée est donc de capturer la forme géométrique et topologique de chacun des ensembles — à travers leurs connexions, leurs regroupements — puis de comparer ces formes globales. Cette approche s’appuie sur un cadre mathématique, j’ai nommé : la topologie des données.

Jean-Luc Parant, éd. Héros-Limite, 2018.
La topologie des données vise à extraire des « signatures » invariantes des données, robustes face au bruit et aux petites perturbations. Si on a jamais entendu parler de topologie, c’est un point à éclaircir : c’est, en gros, l’étude des propriétés des formes qui sont préservées même si l’on déforme ces formes de façon continue, sans les déchirer ni créer de nouveaux raccords. Il faut imaginer des objets comme des « trucs » en latex que l’on peut étirer, gonfler, extruder de façon continue. Tant qu’on ajoute pas ou supprime pas de trous, alors on a toujours, topologiquement parlant, la même structure. La Topologie des Données (en anglais TDA) utilise des concepts comme l’homologie (l’étude des trous) pour quantifier précisément ces « trous » (pouvant être de dimension 3 — des cavités — ou… de dimension supérieure) et comprendre comment ils émergent et disparaissent à différentes échelles dans nos données. En topologie, on étudie des voisinages et des déformations (homéomorphismes), ce qui peut nous intéresser dans les métiers de la documentation.
En effet : sans être un topologue ou un algébriste experimenté, on peut avoir l’intuition de l’utilité de cette approche. Et notamment pour qui travaille dans le contexte patrimonial où les données sont globalement connexes (soit directement avec des graphes, ou indirectement avec leur sémantique), structurées (arbres, graphes, tables, structures fractales, etc.), bruitées (images numérisées, OCR, HTR, doublons). On peut imaginer des applications de classification ou de diagnostic de jeux de données pour éventuellement spécifier différentes pipelines de traitement (et enfin préparer une campagne de normalisation, indexation, etc.). Ou encore — est-ce un château en Espagne ? — pour généraliser un protocole d’évaluation pour un type de données (« pour quel type de document mon évaluation marche ? », « quel est le domaine d’applicabilité de ma méthode ? »).
Cependant, j’insiste : la TDA n’est pas non plus la panacée. C’est un outil intéressant de diagnostic, qui permet de dégager des faisceaux d’indices dans des analyses — mais pas vraiment des preuves. C’est un moyen d’avoir un paysage global de la « tête » de nos données.

Si cela semble être un peu niche dans le domaine des archives/de la documentation (du reste si vous connaissez des articles, je suis preneur), la topologie appliqué aux données semble être une bonne flèche à confier à son carquois d’ingénieur documentaire — comme le transport optimal par ailleurs.
EDIT : Mes intuitions rejoignent finalement le travail de Bayrem Kaabachi &Simon Dumas Primbault, sur la modélisation des régimes de navigations sur Gallica : https://ceur-ws.org/Vol-3558/paper935.pdf. Mais il est parfois bon de tracer son sentier à côté de ceux déjà balisés !
Quelques sites
Tout d’abord, une sélection de vidéos explicatives sur la topologie si vous ne voyez pas de quoi je parle. Elles sont vraiment intéressantes et très didactiques :
- Thomaths 7a. Topologie élémentaire : https://www.youtube.com/watch?v=gfU1TMyF-Bg&t=570s
- Topologie, introduction générale (Maths Adultes) : https://youtu.be/J2wMxCysvJM?si=NbSiIjv5Y9iPbJTE (C’est cette vidéo qui m’a motivé à aller plus loin)
- « Un rond est aussi un carré », (Arte) : https://youtu.be/czY7sp5c_Xs?si=JxGJgYqzqdynlrbB
- Ensuite, surtout, je vous recommande vivement cette vidéo du Collège de France, présentée par F. Chazal où les rudiments de la Topologie appliquée au traitement des données sont exposées de façon claire :
- De façon plus secondaire, le livre « Topologie. L’infini maîtrisé » de Laurent Vivier aux éditions le Pommier. Trouvable d’occasion. Le livre développe plutôt la notion de limite, mais les pages sur la notion de distance et d’espaces m’ont semblé plutôt clairs.
Complexes et boules de gomme (simpliciales)
Il est intéressant de voir qu’historiquement, la topologie naît avec un problème qui a été résolu avec des graphes (Euler et le problème des sept ponts). Comme l’histoire de la topologie, on va commencer avec des sortes de graphes : les complexes simpliciaux. Alors qui sont-ils ? Quels sont leurs réseaux ?
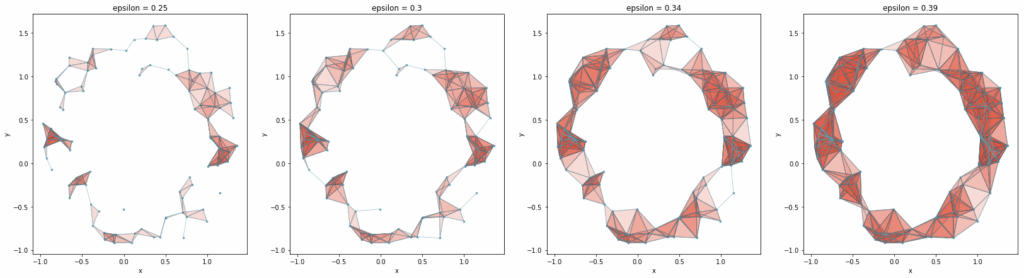
Sans avoir la prétention d’être synthétique ET d’avoir un propos didactique sur la pipeline de la topologie appliquée au traitement des données, je résume grossièrement : il s’agit 1) de transformer nos données en un nuage de points; 2) pour chaque point, d’étirer des zones de collision qui, lorsqu’elles se touchent font naître des lignes pouvant former des triangles ou des formes plus complexes; 3) d’étudier l’apparition de connexions et de trous. L’espace du « devenir-relationnel » des points, c’est le complexe simplicial. C’est comme si l’on commençait par regarder des étoiles pour en dégager des constellations et imaginer des surfaces et des vides spatiaux. (La métaphore cosmique n’est pas si gratuite que cela, car on utilise bien ce genre de stratégie pour étudier les filaments de galaxies et la répartition du vide.)
On dit de cette pipeline, qui consiste à dégager un indicateur via l’étude des connexions, des boucles, et des trous, qu’elle est l’étude des persistances homologiques. Le point 2) est une étape qu’on appelle la filtration.
Bref : on étudie donc un grand ensemble (une filtration sur le complexe simplicial) contenant tous les instantanés (sous-complexes simpliciaux) resituant les mouvements de liage et d’agrégation selon un paramètre (un seuil) de distance qui évolue progressivement. Il est en général noté $\epsilon$. C’est cette évolution qui commence avec des points séparés et qui terminent par des boules « agrégeantes » qui expriment la forme des données. On regarde (et on compte) les trous, les boucles qui se forment. Quand on parle de trous, on parle ici d’homologie et on utilise les nombres de Betti (voire les polynômes de Poincaré) pour les dénombrer. Il faut avoir en tête qu’on ne cherche pas la meilleure configuration simpliciale possible — on ne cherche pas à trouver le meilleur instantané — mais on regarde bien le film, l’ensemble des instants, pour en comprendre la structure. On regarde comment s’individuent un ensemble de composantes pour ne former, à la fin et jusqu’à l’infini, qu’une seul et unique constellation compacte, sans trou.
Mais une image vaut mieux qu’un long discours :


Cette représentation, donc, évolue au fur et à mesure qu’on varie le seuil de connexion (par exemple la taille de la « boule » autour de chaque point) et ce sont les formes (les pâtés de boules) qui émergent modulo ces variations qui donne la signature topologique d’un ensemble de données. En $h_0$, on compte les composants solidaires (points ou paquets de points; en $h_1$ les boucles; en $h_2$ les cavités (comme dans le gruyère). Notez que les visualisations ci-dessus ne représentent pas ces cavités.
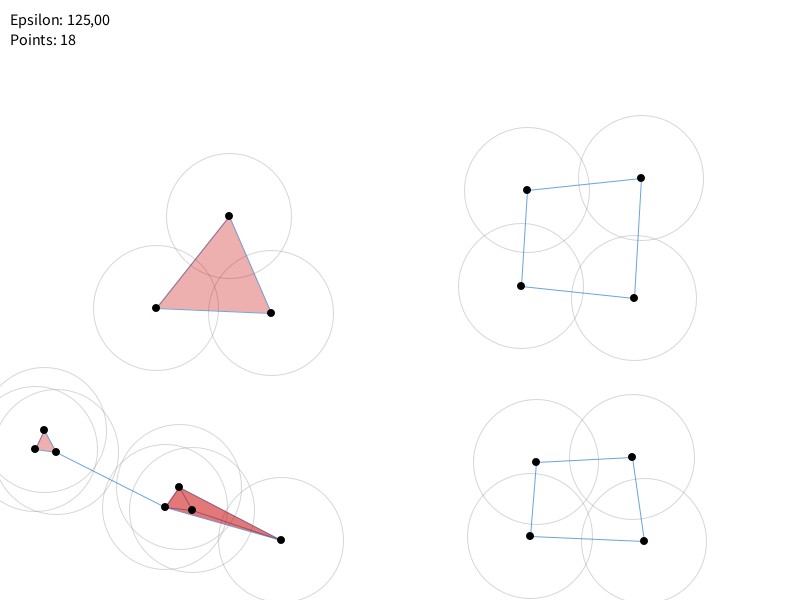
Concrètement, pour $\epsilon = 0$, $h_0$ est égal au nombre de points dans le plan (on aura $n$ « 0-simplexes »). Si dans cet ensemble, deux points très proches fusionnent lorsque $\epsilon$ augmente, alors on aura $n-1$ points puisque cette fusion — formant une ligne — compte maintenant pour un seul élément (on aura donc au total $n-1$ 0-simplexes et $1$ 1-simplexe). Si nous avons maintenant un troisième point qui se joint à la fusion — notre $\epsilon$ augmentant — nous aurons donc une nouvelle entité « remplie », formant un triangle (un 2-simplexe).

Je suppose ici que nous sommes dans le complexe de Rips (peu importe les détails) mais en tout cas cela veut dire qu’on ne peut pas avoir de trou pour trois points reliés; et qu’on ne pourra compter un trou ($h_1 = 1$) qu’à partir de quatre points reliés (on a donc une boucle). Ces $n-simplexes$ naissent et meurt à mesure que $\epsilon$ augmente.
L’avantage du complexe de Rips par rapport à d’autres configurations simpliciales et sa complexité calculatoire moindre par rapport à l’implémentation du complexe de Čech qui prend en compte aussi l’intersection des boules topologiques. Mais ces précisions ne sont pas cruciales pour nous : restons-en au complexe de Rips.
La naissance, la persistance, et donc la mort d’une ou des formes (de « pâtés de boules ») nous racontent des caractéristiques propres aux données. On établit, en faisant grossir nos formes, une série d’instantanés — comme si on établissait des photogrammes qui formeront une sorte de… film de boules. En surenchérissant la métaphore : chaque jeu de données peut livrer une sorte de complexe-tape. (Pardon.)
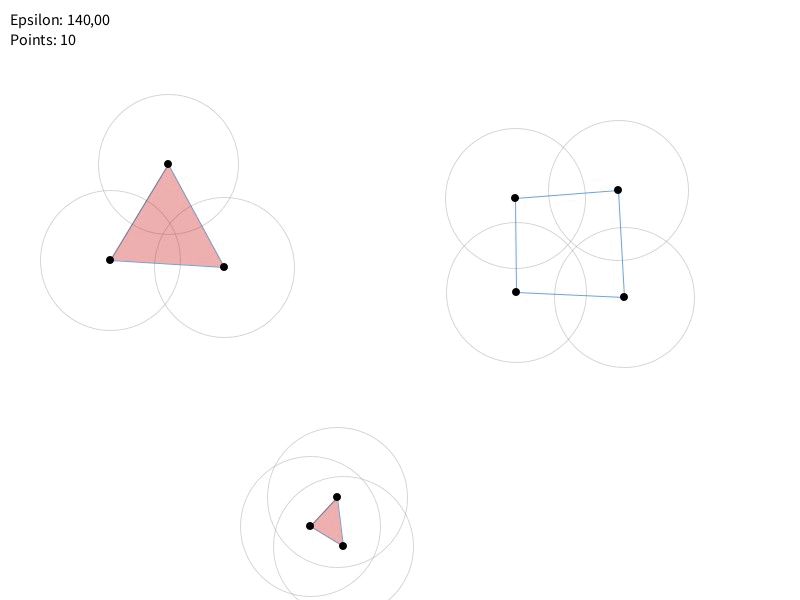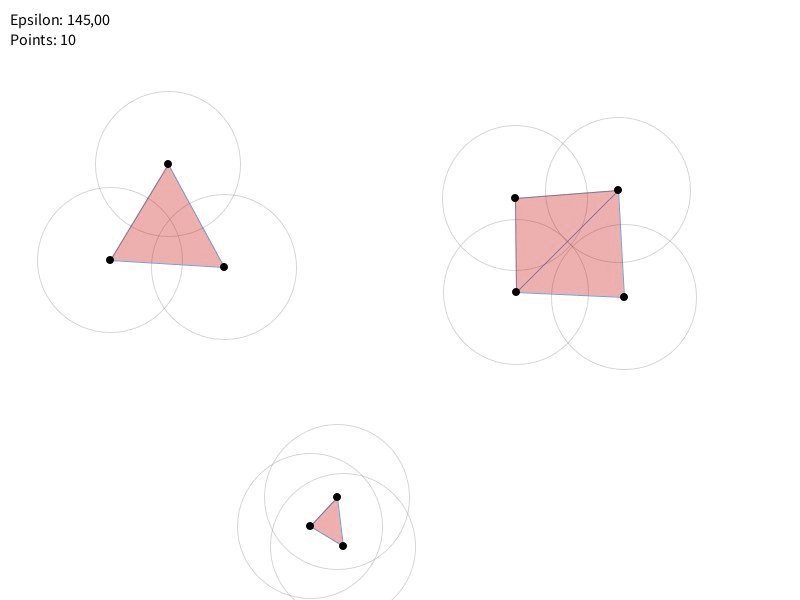
J’insiste sur la logique de la vie et mort des éléments de notre complexe simplicial, au fur et à mesure que le paramètre de filtration $\epsilon$ (qui représente une distance ou un rayon) augmente.
Pour la dimension 0 (en gros H0 = Composantes Connexes) : au départ, pour un $\epsilon$ très petit (proche de 0), chaque point de notre ensemble de données est considéré comme une composante connexe isolée. Si nous avons, par exemple, 10 points, nous observons la naissance de 10 composantes connexes au seuil de filtration $\epsilon = 0$. À mesure que $\epsilon$ augmente, les points se rapprochent virtuellement et des arêtes (1-simplexes) se forment entre eux. Lorsque des arêtes connectent des composantes connexes distinctes, celles-ci fusionnent. La règle est que la composante la plus « jeune » (celle qui a la plus petite valeur de naissance) est absorbée par la plus « ancienne », et ainsi la composante la plus jeune meurt. Ce processus réduit le nombre total de composantes connexes.
Par exemple, si nous avons trois points très proches formant un premier groupe, et trois autres points formant un second groupe, à un certain $\epsilon$, ces groupes internes se stabilisent comme des composantes. Lorsque $\epsilon$ devient suffisamment grand pour relier ces deux groupes entre eux, une des deux composantes (la « moins persistante » ou « plus jeune ») meurt, et le nombre de composantes connexes diminue de un.
Enfin, lorsque $\epsilon$ tend vers l’infini, toutes les composantes finissent par fusionner pour former un unique complexe connecté. Seule cette dernière composante connexe, née à $\epsilon=0$, persiste « à l’infini ».
Pour la dimension 1 (en gros, H1 : Trous ou Boucles) : les caractéristiques de dimension 1, appelées trous ou boucles, suivent une logique similaire. Une boucle (un cycle de 1-simplexes non rempli) naît lorsque des arêtes se connectent de manière à former un chemin fermé qui n’enferme pas encore de « surface » (pas de 2-simplexe remplissant l’intérieur). Par exemple, si quatre points forment les sommets d’un carré et que les arêtes se créent, nous avons la naissance d’un trou. Ce trou meurt lorsque, à une valeur de $\epsilon$ plus grande, le complexe se densifie et qu’un 2-simplexe (comme un triangle ou un carré rempli) se forme et « remplit » ce trou. Le trou n’existe alors plus.
La « vie » d’un trou est donc l’intervalle de filtration entre sa naissance et sa mort. Les trous qui persistent longtemps sont considérés comme des caractéristiques structurelles importantes des données.
A ce stade, on voit qu’il y a un moment crucial : comment transformer nos données en points ? Pour des valeurs numériques, comme des vecteurs rien de plus simple. Mais dans notre cas, avec nos JSONs, on aura petit un défi à relever. Mais finissont-en avec l’exposition des bases de la TDA.
Pour résumer : Le dénombrement de composantes connexes (morceaux ou réseaux) appartiennent au groupe homologique 0 ($h_0$), les boucles à $h_1$… et on peut généraliser à $h_n$ mais ce n’est pas le propos ici.
Les petits trous du poinçonneur des Lilas sont en fait tous des trous de première classe ($h_1 $).

Ce qu’il faut retenir de tout cela : quand naît une mise en relation (la fusion de deux simplexes). On note alors les naissances et les morts des éléments $h_0, h_1, h_2…$. Ce qu’on obtient alors, ce sont des diagrammes de persistance : des ensembles de points qui racontent, pour chaque dimension topologique (connexité, cycles, cavités…), quand ces caractéristiques apparaissent et disparaissent. Ces diagrammes sont comme des empreintes digitales des formes des données.
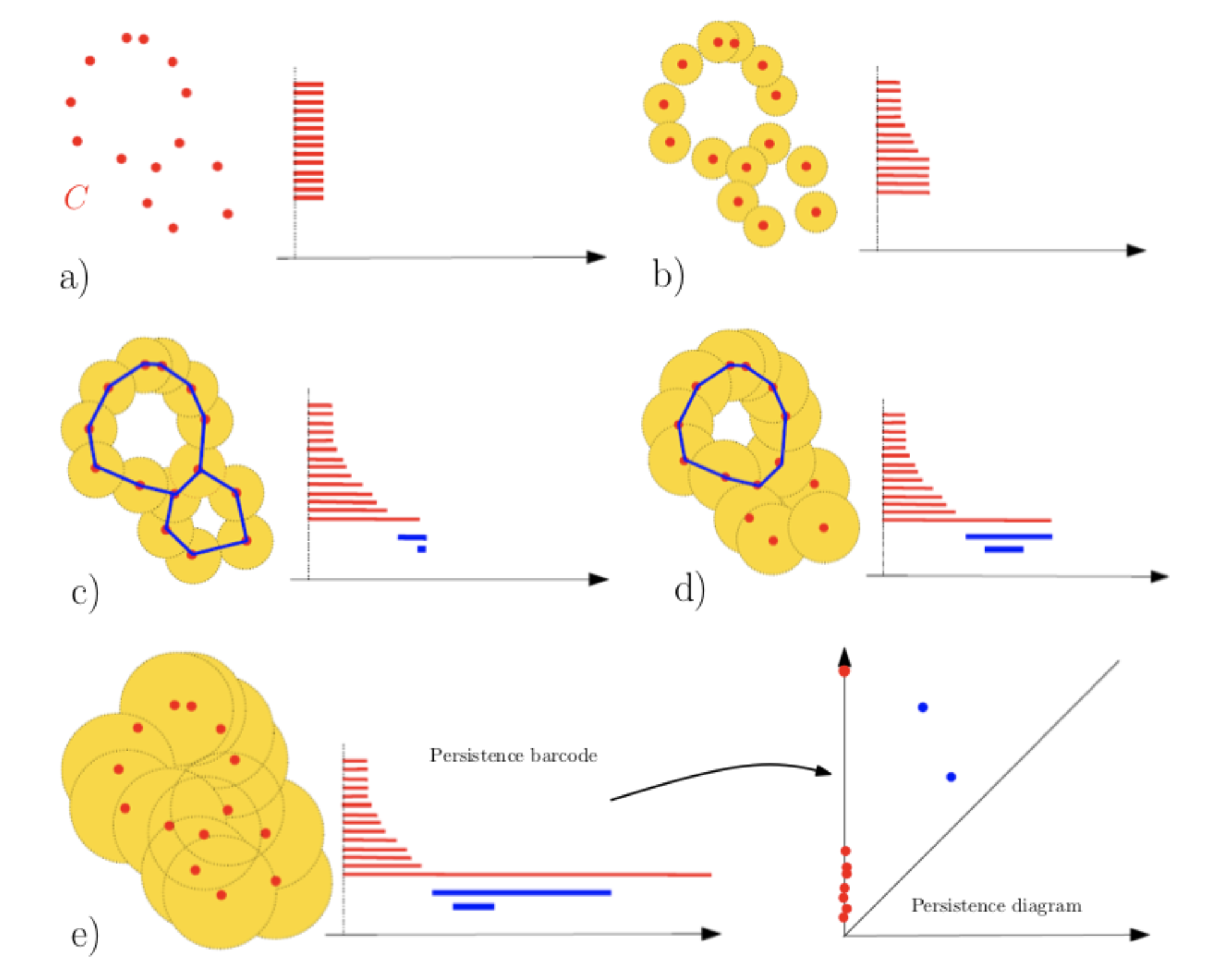
De fait, nous n’aurons pas des données avec des topologies trop complexes et nous nous contenterons de ne pas dépasser le groupe homologique $h_1$. On sous-exploite l’approche topologique — mais piste à explorer, et en particulier pour les données en graphe avec une dimension sémantique. On pourrait imaginer quelque chose avec les thésaurus matière en rdf.

Je m’excuse de ne pas pouvoir me dédier ici à une explication plus étendue des bases de la TDA. En particulier à la méthode du code-barre qui illustre bien la persistance homologique; et la logique de la vie et la mort de structures simpliciales. Je pense cependant que la mise en pratique qui vient sera plus explicite. Il faut juste saisir qu’en appliquant des transformations topologiques sur nos points, en les reliant et en les agrégeant, on obtient une information topologique de nos données. Sinon les vidéos que j’ai présentées le font très bien — ou alors jeter un oeil à celle-ci, plus courte, mais en anglais :
Mise en pratique avec Python
Il est temps de regarder — et comparer — la forme de notre vérité terrain aux données générées par le LLM (via sortie structurée). Si vous ne voyez pas de quoi je parle :
Du JSON à points nommés
On l’a vu, le plus urgent est de transformer nos données en un nuage de points pour jouer avec de façon topologique. Dans notre cas, celui de l’évaluation de la sortie structurée via LLM, nous avons du JSON. Pour rappel, nous avions une vérité terrain qui ressemblait à ça, extrayant l’information des Tables du Sénat, numérisées :
{
"listes_des_intervenants": [
{
"nom": "Babin-Chevaye",
"references_pages": [
8,
582,
719
]
},
{
"nom": "Bachelet (Alexandre)",
"references_pages": "<renvoi d'index>"
},
{
"nom": "Barthou (Louis)",
"references_pages": [
2
]
},
{
"nom": "Barthou (Louis)",
"references_pages": [
394,
396,
397,
399,
1211,
1237
]
},Les données prédites (JSON générés par le LLM), elles, ressemblent à la vérité terrain, mais on se demande à quel point. On voit par exemple que le LLM (ministral 8-b) a factorisé en une les deux entrées « Barthou (Louis) »:
{
"listes_des_intervenants": [
{
"nom": "Babin-Chevaye",
"references_pages": [
8,
582,
719
]
},
{
"nom": "Bachelet (Alexandre)",
"references_pages": "<renvoi d'index>"
},
{
"nom": "Barthou (Louis), ministre de la guerre",
"references_pages": [
2
]
},
{
"nom": "Barthou (Louis)",
"references_pages": [
394,
396,
397,
399,
1211,
1237
]
},Mais comment transformer ces données en points ? Nous ne capturons pas la sémantique textuelle (quoique ce serait intéressant si l’on voulait aussi traiter le contenu textuel des Tables du Sénat), donc exit les embeddings pour notre cas.
Eh bien, comme on l’a fait remarquer dans un des deux premiers articles, une matrice de similarité « interne » — que nous appellerons ici une matrice « tautologique » car elle compare chaque élément d’un ensemble à tous les autres éléments du même ensemble — peut être directement convertie en une matrice de distances (par exemple, en utilisant distance = 1 - similarité). C’est cette matrice de distances qui définit un espace métrique pour notre ensemble de données, nous fournissant ainsi un objet parfaitement compatible avec nos exigences topologiques. Il faut donc calculer deux de ces matrices de similarité tautologiques, puis les transformer en matrices de distances : une pour l’ensemble des données de la vérité terrain, et une autre pour les données prédites par notre modèle. Finalement, ce sont ces matrices de distances qui nous permettent d’exposer clairement les relations de proximité entre nos données, les transformant en un ensemble de points (où chaque donnée est un point) prêts pour l’analyse topologique.
Cela demande un léger effort d’abstraction car on ne positionne pas nos points dans un espace euclidien muni de coordonnées; mais on établit une relation de nature métrique entre différents éléments. Je peux dire (et concevoir) que la Terre est à une unité astronomique du Soleil; que Jupiter est à 5 unités astronomiques du soleil et 4 de la Terre, sans forcément les positionner dans un espace de coordonnées défini. Bien sûr, on peut imaginer un référentiel qui prend a posteriori en compte ces relations, mais c’est un autre problème.
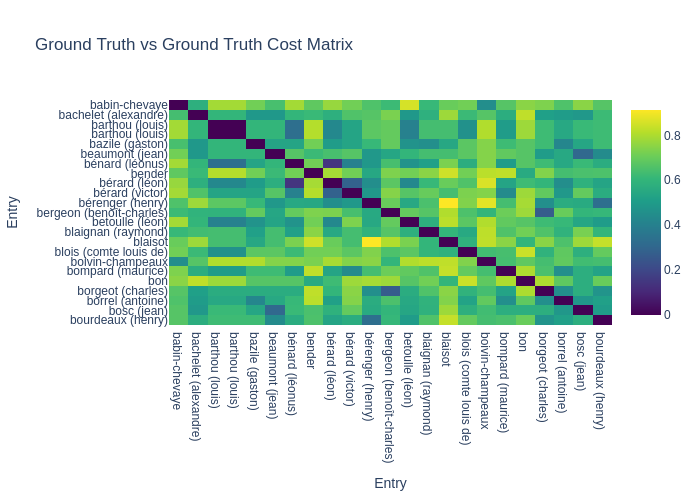
On peut vérifier, on a bien un espace métrique (inégalité triangulaire respectée, symétrie et séparation). On a utilisé la distance de Ratcliff/Obershelp pour avoir des distances normalisées et exporté nos matrices au format .npy.
Si ça vous intéresse j’ai établi une petite démonstration (à mettre au propre) sur la propriété métrique des matrices de similarité tautologiques. Rien de magistral cela dit.
Bien sûr, c’est une approche qui a ses limites car on pourrait imaginer avec des matrices similaires pour des données différentes. Mais dans mon cas, c’est largement suffisant. Encore une fois, on peut imaginer la puissance de l’approche avec des embeddings (par exemple d’un document ou d’une série de documents) car on établit des relations/distances sémantiques de façon interne, comme si les phrases faisaient leur introspection.
Gudhi, change de numéro
Pour faire des manipulations topologiques à partir de nos deux espaces métriques (celle de la vérité terrain et celle des données générées par le LLM), le travail est déjà mâché avec la librairie Python Gudhi. Si on a compris les grandes lignes de la pipeline de la TDA, ce qui va suivre va être assez simple.
Pour l’expérience, j’ai trois ensembles de données: notre vérité terrain et nos données prédites qu’on va comparer (respectivement $a$ et $b$); et des données bruitées ressemblant à des caractères aléatoires ($c$), mais basé sur la même structure JSON (nom + références des pages).
On importe donc les librairies nécessaires (j’expliquerai plus tard pourquoi ot) et on importe nos matrices:
import gudhi
import numpy as np
import ot
a = np.load('cost_matrices_output/gt.npy')
b = np.load('cost_matrices_output/predicted.npy')
c = np.load('cost_matrices_output/noisy.npy')Commençons avec notre vérité terrain pour bien saisir de quoi il en retourne :
rips_complex_gt = gudhi.RipsComplex(distance_matrix=a, max_edge_length=1.0)
simplex_tree_gt = rips_complex_gt.create_simplex_tree(max_dimension=1)
diagram_gt = simplex_tree_gt.persistence()La première ligne initialise un objet RipsComplex dans Gudhi en lui fournissant la matrice de distances entre les points et le seuil maximal de filtration à considérer. Ici, la taille maximale est de 1 car on utilise une distance normalisée. On fait une sorte de « setup topologique », mais sans rien transformer ou traduire notre matrice en objet topologique.
La deuxième ligne va employer ce setup pour construire notre complexe simplicial : on va avoir un objet topologique. On ne dépasse pas la dimension 1, car nos données sont plates. Comme on vise une analyse de la connectivité (le regroupement de nos données), inutile d’aller plus haut.
Ensuite, le tournage de notre « film de boules » se passe à la troisième ligne. C’est ici qu’on va produire l’ensemble des photogrammes de ce film, extrayant les moments clés de naissance et de mort des formes topologiques.
Regardons à quoi ça ressemble avec un print :
print("diagramme de persistance VT (par exmple: [dimension: (naissance, mort))):")
for dim, (birth, death) in diagram_gt:
print(f"Dim {dim}: [{birth:.3f}, {death:.3f})")On a quelque chose comme ça (fragment) :
Dim 0: [0.000, inf)
Dim 0: [0.000, 0.600)
Dim 0: [0.000, 0.556)
Dim 0: [0.000, 0.545)
Dim 0: [0.000, 0.545)
Dim 0: [0.000, 0.515)
Dim 0: [0.000, 0.484)On ne se préoccupe que de la dimension 0. La première valeur entre crochet signifie « la date » de naissance de notre points. J’ai d’ailleurs 23 entrées, donc j’ai bien 23 points. Mais ces points meurent à des dates différentes. Le premier est un peu étrange : [0,000, inf). C’est le cluster le plus grand : car quand epsilon tant vers l’infini, toutes mes composantes (mes points) sont engluées dans les autres. C’est le corps principal du nuage de points. Elle naît également en zéro car elle hérite des vies de chacune des composantes qui, bien entendu, naissent aussi au temps 0.
On fait la même chose avec $b$ (inutile de le faire avec $c$ pour l’instant) puis on stocke les tuples de nos diagrammes dans une variable :
diagram_H0_gt = np.array([pt[1] for pt in diagram_gt if pt[0] == 0])
diagram_H0_pred = np.array([pt[1] for pt in diagram_pred if pt[0] == 0])
On a maintenant des données topologiques prêtes à être manipulées et comparées !
Une première métrique (ambiguë) : la distance de Bottleneck
On a déjà vu par le passé (dans cet article) en quoi consistaient les appariements. C’est une mise en correspondance « optimale » de deux ensembles, de sorte que la somme des coûts soit minimisée (on a la permutation la « moins chère »). S’il y a des permutations moins optimales que d’autres on prend, avec le transport optimal, la meilleure. Mais dans cette meilleure configuration — dans cette somme de coûts minimisée –, il y a peut-être une distance qui est plus coûteuse que les autres ? Eh bien la distance de Bottleneck c’est ça : c’est la pire différence qu’on est obligés d’accepté étant donné notre appariement le plus optimal. Elle nous renseigne sur le coût le plus cher — le pire appariement dans le meilleur des cas. Bref : un score faible veut donc dire « même le pire appariement n’est pas si mauvais que ça ».
Rien de plus simple avec Gudhi :
dist_bottleneck_H0 = gudhi.bottleneck_distance(diagram_H0_gt, diagram_H0_pred)
print("distance de bottleneck : ", dist_bottleneck_H0)Et on obtient :
distance de bottleneck : 0.15384615384615385Comment interpréter ce résultat ? Là je suis moins sûr de moi : il me semble que, dans notre cas et dans notre cas seulement, la distance soit bornée entre 0 et 1 inclus, car on a défini notre diamètre epsilon maximum à 1 — car la distance sur lequel se base notre matrice est une distance normalisée. Mais c’est peut-être une erreur. Dans le cas où cette distance est bien bornée, cela veut dire qu’on peut dégager une métrique « le pire du meilleur » :
$$1 – \text{distance de Bottleneck}$$
Qui pour nous vaut donc environ 0.85 — ce qui est donc un bon score. En permutant mes variables $b$ et $c$ (bref en faisant comme si les données prédites étaient des données bruitées) on a 0.3, ce qui fait une distance de 0.7. Ce n’est pas si horrible que ça.
Comme on le voit, avec les données bruitées, l’écart n’est pas si grand… Donc pas très parlant. Même si un score de 0 (ou très proche de zéro) indiquerait une bonne correspondance. Ici, on est toujours dans une logique « faisceau d’indices ». Un bon résultat est signifiant (si le pire est déjà très bon, alors tout les appariements sont très bons), mais pas un résultat moyen ou mauvais : le mauvais ou très mauvais sont peut-être exceptionnels et pas représentatifs de l’ensemble.
La distance de Wasserstein (ambiguë aussi)
Continuons avec la distance de Wasserstein cette fois-ci, et toujours dans cette idée de comparaison de diagrammes de persistance. Cette distance calcule la somme des coûts de la permutation la plus optimale. C’est donc la valeur de la meilleure configuration. Comme pour la distance de Bottleneck, elle est liée au transport optimal.
En réalité, c’est un peu plus compliqué que ça, car les distances de Wasserstein peuvent être d’ordre $p$. J’ai personnellement choisi $p = 1$ car je ne crois pas qu’on ait besoin d’une sorte de pénalité quadratique pour le calcul des coûts. Et ça permet de calculer plus facilement une borne : en effet, si mes distances maximales sont de 1, ça veut dire que la pire configuration, c’est 23 (le nombre d’entrées) fois 1 (la distance maximale possible). J’aurais donc à diviser ma distance de Wasserstein par 23 (qu’on note $n$). Ensuite, il n’y a plus qu’à faire
$$1 – \text{distance de Wassertein}_1$$
Ce qui donne :
dist_wasserstein_H0 = wasserstein_distance(
diagram_H0_gt, diagram_H0_pred, order=1.0, internal_p=2.0
)
print(f"Distance de Wasserstein (H0): {1 - (dist_wasserstein_H0 / n)}")On a vu order, `internal_p, désigne ici la façon dont on calcule les distance : 2, c’est pour la distance euclidienne, et ça me semble correct (à discuter).
Entre notre ensemble $a$ et $b$, on a donc un score de similarité de $0.97$. Et pour notre ensemble bruité on a environ $0.5$. Très bon score pour la vérité terrain vs. données prédites, donc; et score médiocre pour $c$. Concrètement, ça veut dire que pour le premier score, le LLM reproduit la structure de connectivité (en $H_0$, toujours) de la vérité terrain avec une précision fort appréciable. Les temps de fusion des composantes connexes dans les prédictions sont extrêmement proches de ceux de la vérité terrain.
Encore une fois, ces métriques sont à prendre avec des pincettes… Par exemple, il me semble difficile d’avoir un résultat qui avoisine les 0, même avec beaucoup de bruit. Bref, le score est sans doute moins sensible aux extrémités. Je ne sais pas. Je ne suis pas sûr de moi à propos des bornes non plus, même si on posant et en reposant le schmilblick, je ne vois pas comment ça pourrait dépasser 1.
Des « courbes » de Betti
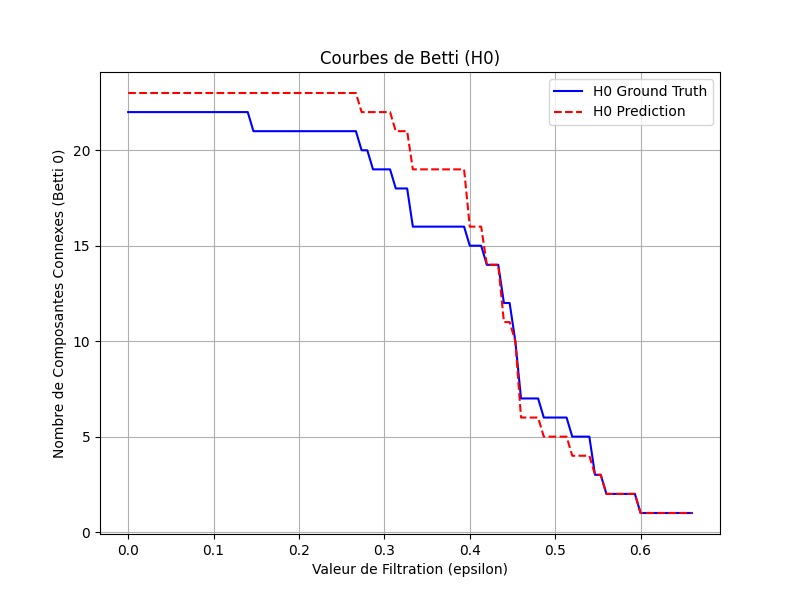
Ici, on va enfin pouvoir exploiter les informations homologiques de nos ensembles et avoir des résultats plus visuels. On va utiliser une « courbe » de Betti pour $H_0$ (le « nombre de composantes connexes ») qui montre comment le nombre de groupes connectés évoluent à mesure qu’on augmente la valeur de filtration $\epsilon$. Évidemment, ce n’est pas vraiment une courbe puisqu’on a affaire à des ensembles discrets — on a donc affaire à une fonction qui produit un escalier.
On pourrait s’amuser à établir des interpolations pour approximer une vraie courbe mais ça paraît un peu « overkill » 😀 . Cela dit, pourquoi pas, cela permettrait d’étudier la dynamique des changements qualitatifs brutaux (les changements de rythme des fusions) en dérivant la fonction obtenue… à voir si c’est vraiment pertinent.

Pour ce faire, on va donc transformer nos informations de naissance et de mort sur un graphique au regard de $\epsilon$. On l’a vu, $\epsilon$ tend vers l’infini, ce qui n’est pas convenable pour une représentation graphique. Il faut donc définir une intervalle (« l’espace ou plage de filtration ») pour notre fonction de Betti ou $\epsilon$, en abscisse, joue le rôle de la variable incrémentale, similaire au $t$ des physiciens ou du $x$ traditionnel des fonctions mathématiques. En ordonnée, on aura donc le nombre de composantes connexes. Cette fonction va donc représenter l’évolution des fusions des éléments $h_0$.
Mais on ne va pas représenter tous les $\epsilon$, car il y a un moment où la forme est infiniement stable, le moment où il ne reste plus qu’une seule composante. On va donc juste regarder la partie du film qui commence avec toutes nos composantes connexes « seules » (l’instant 0) et qui termine au moment où l’on a tout fusionné. Il faut donc stocker d’une part la valeur la plus grande (celle qui fait « embrasure » avec l’infini) et les autres qui sont finies et ajouter une petite marge de 10% pour être large. On échantillone notre espace de filtration avec une granularité de 100 — on fait la même chose pour la vérité terrain et les vérités prédites; mais on garde la même plage de filtration :
max_finite_val_H0 = 0
max_finite_val_H0 = max(max_finite_val_H0, np.max(diagram_H0_gt[np.isfinite(diagram_H0_gt)]))
max_finite_val_H0 = max(max_finite_val_H0, np.max(diagram_H0_pred[np.isfinite(diagram_H0_pred)]))
n_steps = 100
filtration_values = np.linspace(0, max_finite_val_H0 * 1.1, n_steps)
Maintenant, pour visualiser l’évolution de la topologie de nos données, nous construisons la fonction compute_betti_curve qui prend en entrée un diagramme de persistance (une liste de paires (naissance, mort) pour chaque caractéristique topologique) et une série de valeurs de filtration (les $\epsilon$ qui définissent nos « instantanés ») :
def compute_betti_curve(diagram, filtration_values):
betti_curve = []
for t in filtration_values:
count = 0
for birth, death in diagram:
if birth <= t and death > t:
count += 1
betti_curve.append(count)
return np.array(betti_curve)Pour chaque $\epsilon$, elle compte le nombre de caractéristiques topologiques qui sont « vivantes » à ce moment précis, c’est-à-dire celles qui sont nées à un $\epsilon$ inférieur ou égal à la valeur actuelle, et qui ne sont pas encore mortes. Ce comptage nous donne le nombre de Betti pour cet $\epsilon$. En répétant ce processus pour toutes les valeurs de filtration, on obtient la « courbe » qui illustre comment le nombre de composantes connexes (pour H0) ou de trous (pour H1 et au-delà) varie à mesure que la connectivité de nos données augmente.
Enfin, il ne reste plus qu’à utiliser la fonction pour nos données et afficher la courbe :
betti_H0_gt = compute_betti_curve(diagram_H0_gt, filtration_values)
betti_H0_pred = compute_betti_curve(diagram_H0_pred, filtration_values)
plt.figure(figsize=(8, 6))
plt.plot(filtration_values, betti_H0_gt, label="H0 Ground Truth", color='blue')
plt.plot(filtration_values, betti_H0_pred, label="H0 Prediction", color='red', linestyle='--')
plt.xlabel("Valeur de filtration (epsilon)")
plt.ylabel("Nombre de composantes connexes, Betti_0")
plt.title("\"Courbes\" de Betti H_0")
plt.legend()
plt.grid(True)
plt.show()Ce qui donne :

Ainsi, en comparant la courbe H_0 Ground Truth (bleue) et la courbe H_0 Prediction (rouge), on peut visualiser comment la structure de connectivité des données prédites se comporte par rapport à celle de la vérité terrain. Les courbes semblent proches (elles ont le même rythme) et c’est plutôt bon signe. On voit que la courbe rouge des données prédites à plus de composantes connexes au début, ce qui veut dire que le LLM a halluciné — ou produit davantage d’entités — que dans la vérité terrain. Si on voit des similarités dans le comportement des deux courbes — elles semblent se « traquer » –, on ne peut pas vraiment conclure, à défaut de métrique. On pourrait imaginer utiliser une DTW (pour Dynamic Time Warping) pour mesurer la similarité des suites entre ces deux « parcours homologiques ». Mais avant cela, comparons avec des données bruitées, aléatoires (notre ensemble $c$) :
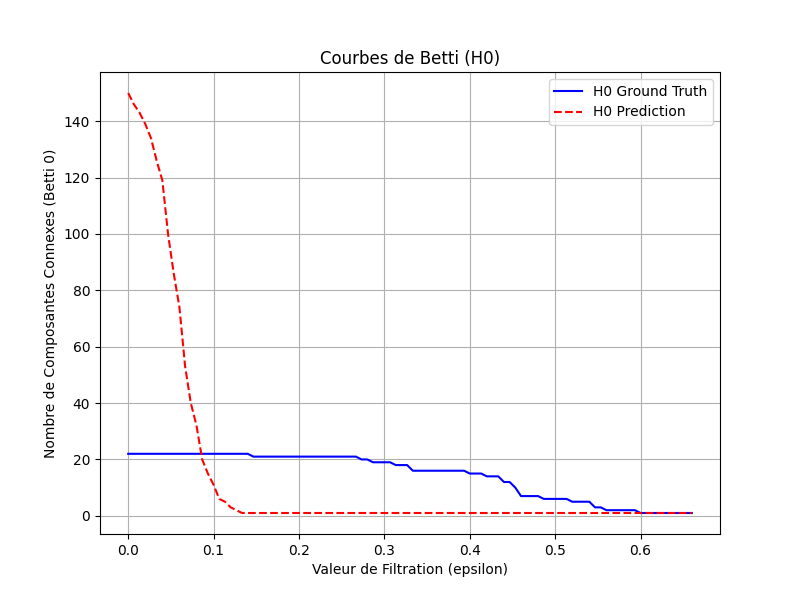
On voit que les courbes n’ont pas du tout la même forme, pas le même « rythme ». La courbe rouge semble subir une unique catastrophe (elle s’effondre) quand la bleue de la vérité terrain semble dérouler un escalier. Elles ne se « traquent » pas du tout, elles n’ont pas la même dynamique « catastrophique ».
Pardon pour ces guillemets trop nombreux ! Mais ici, à défaut de métrique, la métaphore — ou la référence implicite à René Thom, sans doute mal utilisée ici — est une bonne alliée pour sentir la forme des données même s’il faut se méfier du vertige des analogies.
On pourrait calculer les surfaces sous les courbes, retrancher les valeurs pour obtenir une différence, la normaliser. Mais on le voit, les courbes se passent dessus-dessous; donc ces jeux de compensation impliquent des biais et la valeur obtenue ne nous dirait pas grand chose d’utile. Il faut donc user de nouveaux stratagèmes.
Bâtir un score de similarité topologique avec la déformation temporelle dynamique (DTW)
Les métaphores sont malgré tout vecteur d’imagination rationnelle : on voit que les « courbes » se traquent. Alors pourquoi ne pas utiliser l’algorithme du Dynamic Time Warping, utilisé pour calculer la similarité entre deux courbes temporelles et qui gère les différences de « rythme » ?
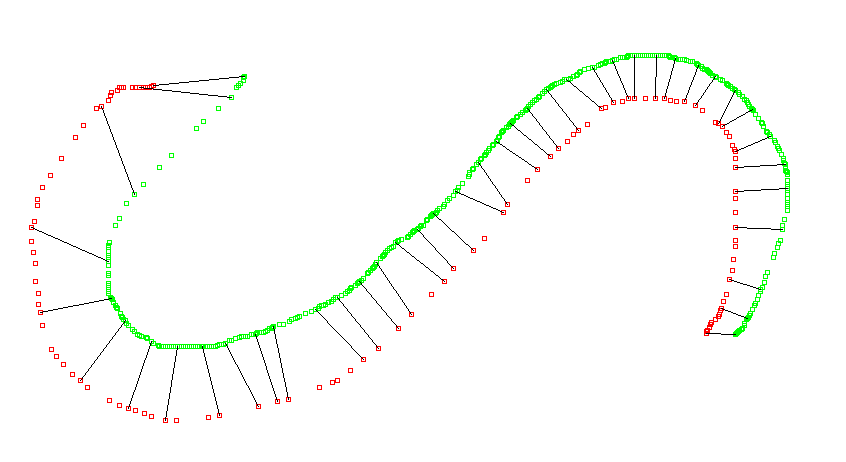
La DTW, pour résumer, est un algorithme qui permet de mesurer la similarité entre deux séquences de données qui peuvent varier en vitesse ou en durée. Contrairement aux méthodes de comparaison directes qui exigent des séquences de même longueur et parfaitement alignées, le DTW est capable de « déformer » temporellement (étirer ou compresser) une séquence pour l’aligner de manière optimale avec l’autre. En minimisant la somme des distances entre les points alignés, il fournit une mesure de la ressemblance globale des formes des deux séquences, même en présence de décalages ou de variations de rythme. Cette flexibilité, on le voit, rend la DTW particulièrement utile pour comparer des évolutions de données où les événements clés peuvent ne pas se produire exactement au même moment — comme c’est le cas pour les courbes de Betti. On l’utilise simplement avec la librairie fastdtw :
distance_dtw, path = fastdtw(betti_H0_gt, betti_H0_pred, dist=lambda u, v: abs(u-v))
print(f"La distance DTW entre les courbes H0 Ground Truth et H0 prédiction est : {distance_dtw}")
Sans entrer dans le détail de l’implémentation de la DTW — ce n’est pas le point — on établit une distance de $59.0$ entre $a$ et $b$; et $1147$ pour $a$ versus $c$. On voit qu’il y a une grande différence entre les données générées et l’ensemble bruité mais… à quel point ? Il faut donc trouver la métrique appropriée.
Pour ce faire, il faut « borner »; il faut avoir un ratio dont la valeur est comprise entre 0 et 1 inclus. Il faut alors trouver la pire courbe « cohérente » où la distance avec la courbe de Betti est maximisée. On pourrait imaginer une « courbe » qui est très haut en $y$ puis chute brutalement quand la courbe rivale tombe à un. Mais la hauteur à choisir serait arbitraire. Je me contente ici de poser que la pire courbe, le cas de divergence maximale, est une simple constante $y = 1$ (à démontrer mais intuitivement satisfaisant 😀 ). Il faut donc aussi calculer la DTW entre le pire cas et la vérité terrain, qui représente le maximum de divergence.
En tout cas : le « pire cas » que l’on peut imaginer est une courbe qui n’aurait aucune dynamique d’agrégation : elle reste obstinément à $y=1$ sur toute l’échelle d’$\epsilon$. Cela signifie qu’elle prétendrait que, dès le départ et pour toujours, toutes nos données ne forment qu’une seule « constellation compacte », sans jamais montrer l’individualisation des groupes à des échelles plus fines. Cette constante $y=1$ se fait donc le parfait reflet d’une divergence maximale par rapport à la réalité topologique de nos données.
Notre métrique, inclue entre 0 et 1, vaut donc :
$$\text{Score}_{\text{DTW}} = 1 – \frac{DTW_{\text{modèle}}}{DTW_{\text{max_divergence}}}$$
Voici la traduction python :
betti_H0_pire_cas = np.full(len(betti_H0_gt), 1.0)
distance_dtw_gt_vs_pire_cas, path = fastdtw(betti_H0_gt, betti_H0_pire_cas, dist=lambda u, v: abs(u - v))
print(f"la distance DTW entre la courbe H0 Ground Truth et la courbe 'pire cas' (y=1) est: {distance_dtw_gt_vs_pire_cas}")
score_dtw = 1 - (distance_dtw / distance_dtw_gt_vs_pire_cas)
print(score_dtw)Ce score, que l’on appelle ici « métrique de similarité topologique via déformation temporelle dynamique » (pourquoi faire plus court ?), mesure la proximité de l’évolution topologique de nos données prédites par rapport à la vérité terrain.
Voici les résultats, plutôt parlants :
- pour vérité terrain versus données prédites, on a $0.95$;
- pour vérité terrain versus données bruitées, on a $0.14$.
On peut donc dire respectivement qu’il y a une similarité structurelle (« formelle » ou « topologique ») de 95% entre la vérité terrain et les données générées; et une similarité de 14% entre la vérité terrain et les données bruitées. Je crois qu’on a atteint le climax de cet article de blog avec le combo DTW + nombre de Betti 😀
Bien que l’idée d’utiliser la Dynamic Time Warping (DTW) pour comparer des courbes dérivées de l’Analyse Topologique des Données ne soit pas révolutionnaire, l’approche fournit une métrique normalisée relativement intuitive pour évaluer la performance du modèle, en tout cas au regard de la structure des données.
Conclusion
On a expérimenté la topologie pour l’analyse des données pour l’évaluation de la sortie structurée de LLM à des fins documentaires. Bien que cet article ne fait que survoler le sujet, on voit que cette approche — peu signifiante toute seule — permet d’intégrer la dimension globale (la forme topologique des données), laquelle enrichit malgré tout l’analyse.
L’utilisation et la comparaison des courbes de Betti avec la métrique de similarité topologique via déformation temporelle dynamique, pourrait également s’appliquer à partir, non pas de matrices de similarité métriques, mais d’une information sémantique encodée (embeddings). Ce qui permettrait de comparer et d’analyser l’état (donc la forme) des données à une étape de leur traitement, utile par exemple dans des tâches de normalisation documentaire, pour vérifier qu’il y ait pas de pertes informationnelles lors de la transformation de données.
Bref : encore beaucoup de choses à expérimenter, et plus encore dans le contexte documentaire où compte l’intégrité informationnelle — c’est-à-dire : la conservation des rythmes topologiques.
Mais on a aussi de quoi se demander : « le jeu en vaut-il la chandelle ? ». Bien que ça ne soit pas spécialement difficile à coder grâce aux librairies qui nous mâchent le travail, cela permet de dégager des métriques difficiles à interpréter, voire ambiguës. Ces métriques n’ont pas vraiment valeur de preuve, mais donnent des indices sur « la forme » des données — notion qualitative étrange, en contexte topologique, — qui demande déjà un petit effort d’abstraction. Sans doute faut-il voir la topologie comme un outil « en plus »,intellectuellement stimulant, mais qui ne pourra jamais renverser la table des habitudes.
👉 Retrouvez le code de cette expérimentation sur Github : https://github.com/desireesdata/exp-evaluate-structured-output-via-LLM-with-topology
Laisser un commentaire