On peut utiliser des modèles génératifs pour indexer — et donc extraire a posteriori — le contenu de textes en les interrogeant et en les contraignant avec de la sortie structurée ou de la génération structurée. Mais il peut y avoir du sable dans l’engrenage : les LLMs peuvent se tromper par exemple en oubliant d’indexer telle ou telle entité d’un texte donné. Comment alors évaluer la qualité d’une extraction sémantique ou, autrement dit, sa façon d’attribuer des bonnes étiquettes aux bons mots ? Est-ce qu’il y a des mots ou des étiquettes en trop ? des informations oubliées, etc. ? Il se trouve qu’un vieux problème de 1781 à propos de tas de sables et de trous nous donne des éléments de réponses…
Je suis actuellement en stage pour le projet Mezanno à la Bibliothèque nationale de France (BnF) et l’EPITA, dédié à l’annotation automatique de documents sériels numérisés et à l’extraction de données structurées. Dans ce contexte, je travaille sur une méthodologie d’évaluation des données générées à partir du Journal Officiel disponible sur Gallica. Cet article de blog, comme le précédent qui établit des éléments plus historiques, est un moyen pour moi de mettre à plat ce face à quoi je suis confronté, aussi bien vis à vis des aspects documentaires que techniques.
Aujourd’hui c’est ce dernier aspect qui m’intéressera : car il sera question de parler de l’évaluation des LLMs utilisés pour des tâches de type « indexation » — concrètement ajouter une couche sémantique ou une référence à une ou des informations pour pouvoir les retrouver plus facilement ou bien pour y effectuer des traitements numériques. Cette première partie est consacrée à la clarification des enjeux et des pistes suivies pour évaluer les résultats de la sortie structurée.
L’évaluation des résultats est extrêmement importante et notamment pour les usages scientifiques des LLMs. Si on utilise les résultats d’une indexation produite par un LLM, on veut savoir quelles sont les marges d’erreurs, éventuellement pouvoir les localiser et d’avoir une idée de ce qui les provoque. Si, par exemple, on peut utiliser les modèles génératifs pour extraire des informations importantes contenues dans des archives, l’historien.ne qui les utilise veut pouvoir motiver les résultats obtenus en en connaissant les limites et les assises.
Je l’annonce d’emblée : cette méthode d’évaluation des LLMs peut être abordé avec le de transport optimal — j’y reviendrai plus bas — problème qui a été formalisé par le mathématicien français Gaspard Monge dans son Mémoire sur la théorie des déblais et de remblais en 1781. Le transport optimal, d’ailleurs, prend aujourd’hui un « coût de neuf »1 avec ses applications numériques ou encore en physique (comme la mécanique des fluides) ou en biologie (pour l’analyse du contenu génétique des cellules)2.

Voilà que l’affaire de Monge à propos de brouettes remplies de sable rejoignent aussi nos préoccupations documentaires actuelles, à savoir celles de l’évaluation des données produites par des modèles génératifs pour l’indexation de corpus textuels.
Un avertissement : j’ai tenté avant tout de produire des « stratégèmes allusifs » pour expliciter les concepts que j’utilise indirectement via des librairies Python et cela bien qu’ils soient, sans doute, assez rudimentaires pour l’étudiant en mathématiques ou en informatique. C’est un moyen de mettre les choses au clair pour moi-même.
LLMs et indexation : l’approche de la sortie structurée, génération structurée
Avant de parler des stratégies d’évaluation, je dois d’abord revenir sur la sortie et la génération structurée.
Parmi les façons d’utiliser la capacité de compréhension des LLMs pour des tâches d’extraction d’entités nommées, on trouve ces deux approches. Leur philosophie générale repose sur la mise en contrainte du LLM pour qu’il fournisse un texte formaté, par exemple en le forçant à adopter une grammaire particulière comme le JSON.

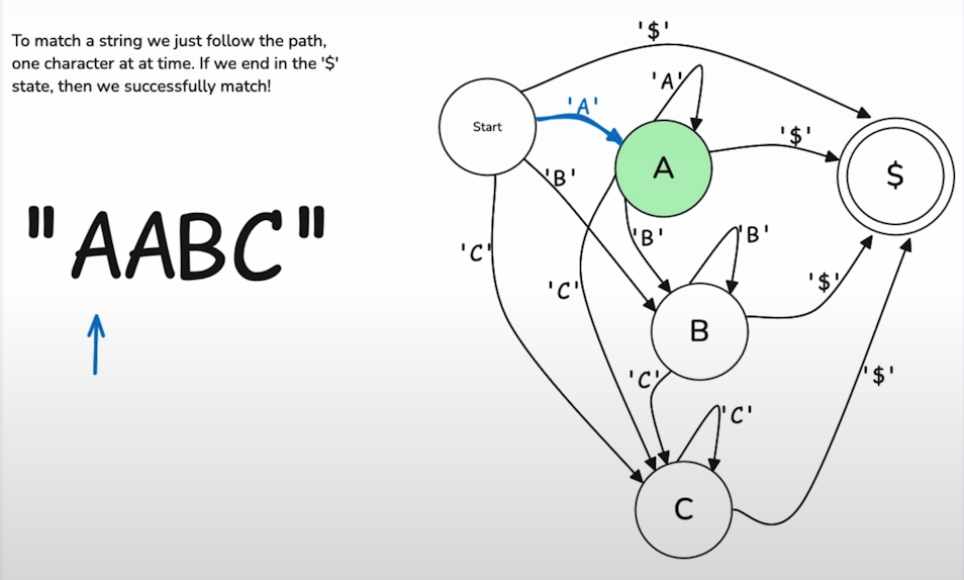
En effet, les modèles génératifs, comme ChatGPT, produisent du texte sans que l’on sache à l’avance quel chemin discursif ils vont emprunter. Chaque « mot » est choisi en fonction des probabilités (logits) qui suivent le mot précédent. Par exemple, après le mot « le chat », le modèle pourrait avoir une certaine probabilité de choisir « mange » et une autre probabilité de choisir « miaule ». Si « mange » est sélectionné, les probabilités pour les mots suivants pourraient inclure « la » ou « du », puis « la souris » ou « du lait », etc. Si c’est « miaule », alors « fort » pourrait être une option probable. Chaque nouveau mot implique donc une sorte de reconfiguration du chemin, un peu comme un sentier qui se redessine au fur et à mesure. Cette distribution des probabilités dépend du mécanisme d’attention, qui permet au modèle de se concentrer sur les parties les plus pertinentes des données d’entrée. Si on demande ainsi à un LLM ce que mange le chat, il ne va pas nous parler de miaulements car son « attention » aura été portée ailleurs.
Il peut donc être très utile de contraindre un LLM avec des « chemins discursifs » déterminés en amont pour obtenir une réponse formatée, qui facilitera le traitement que l’on pourra y faire a posteriori. En effet, une réponse « prolixe », dans le langage naturel, n’est pas forcément adéquate par exemple pour des tâches d’indexation où l’on veut étiqueter des données pour les retrouver ou pour les traiter. Une réponse sous le format d’un dictionnaire (JSON) est plus qu’approprié.
La sortie structurée, laquelle repose sur la soumission implicite d’un modèle à suivre, permet de contraindre un LLM à exprimer ou ajuster une réponse dans un certain format qu’il a par exemple rencontré lors de son apprentissage. On va « guider » la réponse avec un format de sortie.
Quant à la génération structurée, elle permet aussi de faire de la sortie structurée en contraignant les logits (en gros les probabilités rattachées aux « mots » qui peuvent être tirés) en lui soumettant une structure syntaxique que le modèle génératif devra suivre — comme si on avait nivelé certaines ravines d’une chréode pour ne garder que les sentiers pertinents, balisés. Entre sortie et génération structurée, il y a une subtile différence, mais retenons que la génération structurée permet de faire de la sortie structurée (contrôle fin des probabilités); laquelle peut être intégrée sans implémentation du contrôle des logits grâce aux capacités expressives du modèle qui lui sont intrinsèques.
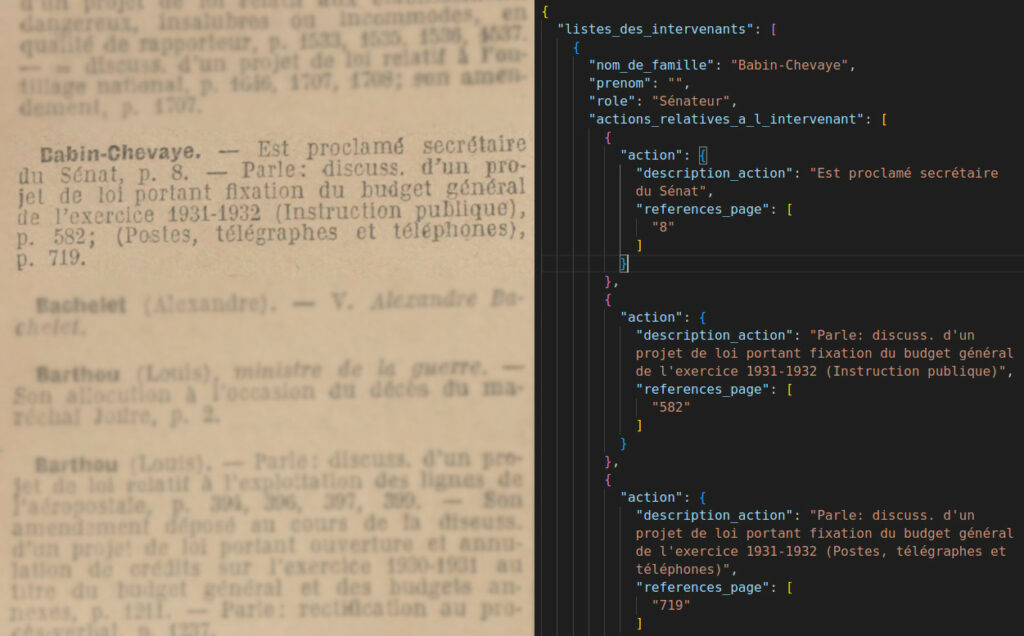
Dans mon cas, j’utilise la sortie structurée sans génération structurée avec la soumission d’un format attaché au prompt. Voici concrètement comment se présente le résultat d’une sortie structurée, générée à partir d’une OCRisation d’une page du Journal Officiel et avec une température nulle (extrait):
{
"listes_des_intervenants": [
{
"nom_de_famille": "Babin-Chevaye",
"prenom": "",
"role": "Sénateur",
"actions_relatives_a_l_intervenant": [
{
"action": {
"description_action": "Est proclamé secrétaire du Sénat",
"references_page": [
"8"
]
}
},
{
"action": {
"description_action": "Parle: discuss. d'un projet de loi portant fixation du budget général de l'exercice 1931-1932 (Instruction publique)",
"references_page": [
"582"
]
}
},
{
"action": {
"description_action": "Parle: discuss. d'un projet de loi portant fixation du budget général de l'exercice 1931-1932 (Postes, télégraphes et téléphones)",
"references_page": [
"719"
]
}
}
]
},
{
"nom_de_famille": "Bachelet",
"prenom": "Alexandre",
"role": "Sénateur",
"actions_relatives_a_l_intervenant": [
{
"action": {
"description_action": "V. Alexandre Bachelet",
"references_page": []
}
}
]
},
{
"nom_de_famille": "Barthou",
"prenom": "Louis",
"role": "Ministre de la guerre",
"actions_relatives_a_l_intervenant": [
{
"action": {
"description_action": "Son allocution à l'occasion du décès du maréchal Joffre",
"references_page": [
"2"
]
}
},
{
"action": {
"description_action": "Parle: discuss. d'un projet de loi relatif à l'exploitation des lignes de l'aéropostale",
"references_page": [
"394",
"396",
"397",
"399"
]
}
},En pratique, cette sortie a été obtenue en adjoignant à un prompt un modèle Pydantic (qui ressemble aux structs des langages C++, Go ou de Rust). Voici à quoi ressemble ce modèle Pydantic — le design du « bon » modèle de données pouvant d’ailleurs à lui seul faire l’objet d’un article — :
class Action(BaseModel):
description_action:str
references_page: list[int]
class Interventions(BaseModel):
action : Action
class Renvoi(BaseModel):
nom_entree_du_renvoi: str
class ReferencesPages(BaseModel):
references_pages: list[int]
class Intervenant(BaseModel):
nom: str
references_pages: Union[list[int], str]
class IntervenantAuSenat(BaseModel):
listes_des_intervenants: list[Intervenant]Je renvoie vers la documentation de l’API Mistral, que j’utilise, si vous voulez avoir une idée de ce à quoi ressemble un programme en entier.
A noter que pour le reste de l’article, je ne travaillerai qu’avec un version réduite de ma vérité terrain et du design du format de données Pydantic : il ne subsiste que les noms et les numéros de page. Mais cela n’a pas d’importance pour l’instant.
Avec quelques lignes de code, on arrive à extraire de façon structurée l’information d’un texte résultant d’un OCR — et, semble-t-il, de façon assez satisfaisante. Mais est-ce que, sur l’ensemble d’une page ou d’un corpus, tout est parfaitement analysé ou est-ce qu’il y a du sable dans l’engrenage ? On pourrait imaginer que les erreurs de l’OCR se répercutent dans la génération de données structurées; qu’un extrait de page, coupée, empêche le LLM de « se concentrer » sur les informations à extraire; qu’il y a des éléments oubliés ou hallucinés ? Bref, le texte généré est-il cabossé, troué ?
Distance et similarité
Une manière d’avoir connaissance de la qualité du travail de la sortie structurée ($E$) est de l’évaluer avec une vérité terrain ($VT$) — une sorte de résultat parfait, que l’on aura fait plus ou moins à la main. Il faut donc comparer $VT$ avec $E$, sachant que l’on exclut pas que les données évaluées $E$ peuvent contenir des oublis ou des éléments hallucinés. Il y a en fait plusieurs choses à prendre en compte et notamment :
- L’existence de tous les éléments (ou nœuds textuels)
- La structure hiérarchique du JSON (il faut comparer des branches)
- L’appartenance de chaque nœud aux bonnes branches
- Le bruit des nœuds textuels eux-mêmes, pouvant être lié à la qualité de l’OCR ou encore les corrections proposées par le LLM
Sur le papier les choses paraissent simples : pour vérifier par exemple si tous les éléments sont présents, il n’y aurait qu’à compter le nombre de nœuds de la vérité terrain et ceux de la version générée, et la division du dernier sur le premier donnait une statistique des éléments pris en compte. Mais cette approche simpliste ne permet pas de prendre en considérer que des éléments peuvent être répétés ou inventés, répartis sur d’autres branches; ou bien agrégés à un autre nœud ou une autre branche. Cette statistique ne serait signifiante à la limite que s’il y avait effectivement plus de nœuds dans la version générée que dans la vérité terrain car cela voudrait dire que le LLM a eu plus de choses à dire que la vérité terrain — dans les faits, ça n’est jamais arrivé. Elle ne permet pas non plus d’avancer dans notre pseudo-cahier des charges des vérifications à faire.
Cette objection me permet de dire qu’un problème a priori simple débouche en fait sur des ramifications car il y a, dès qu’on met les mains dans le cambouis, des cas qu’on avait pas prévu et qu’il faut prendre en considération. L’empilement des exceptions-qu’on-avait-pas-vu-venir implique d’adopter finalement de nouvelles approches plus souples.
Ce que l’on veut, donc, c’est d’avoir une vue générale de la similarité entre nos deux ensembles. Une première approche, simple, est de calculer une matrice de similarité. Une distance de Levenshtein suffit largement car c’est bien la texte généré que l’on évalue — et non pas sa sémantique.
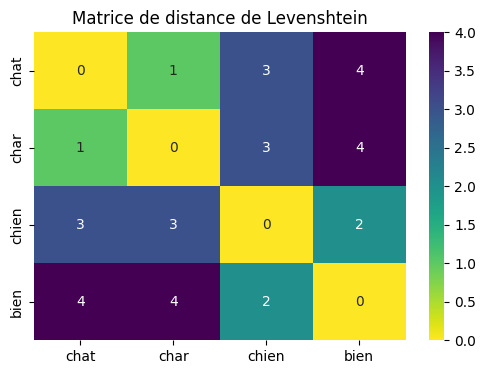
Comme la matrice précédente, la matrice qui suit compare, de façon « aplatie », chaque élément textuel de la vérité terrain avec chaque élément textuel des données générées sans prendre en considération l’organisation du JSON. Plus la distance d’un mot de $VT$ (en $y$) comparé à la donnée produite (en $x$) est basse et nulle, plus le pixel est clair.
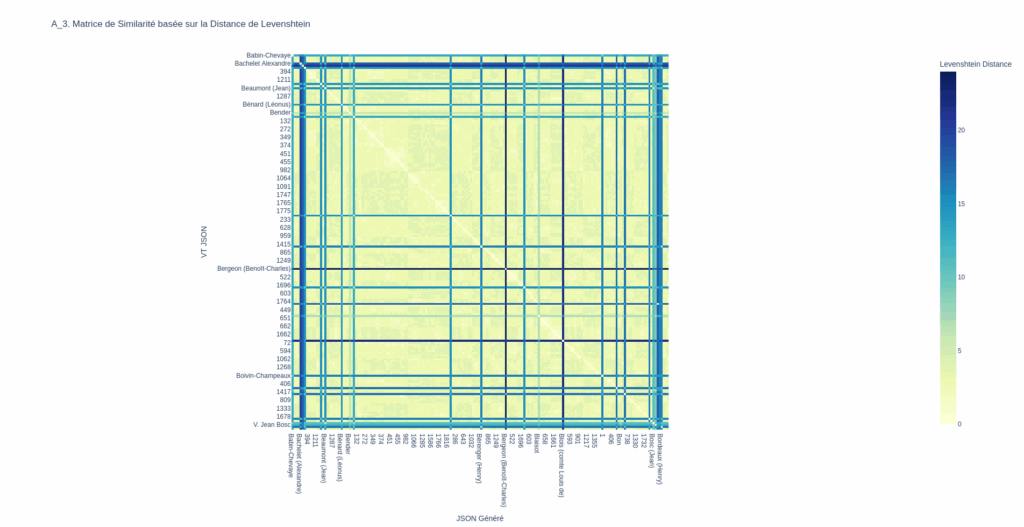
Si on comparerait la VT avec elle-même, on obtiendrait une belle diagonale de zéros, claire, le le n-ième élément en X ayant une distance nulle avec le n-ème élément en Y. Or, ici, on voit que ce n’est pas le cas ; il semble y avoir des décalages de ce genre :

Ce décalage peut vouloir dire que le LLM a loupé des éléments puis s’est resynchronisé.
Les données n’étant pas parfaitement alignées, on a donc besoin de savoir dans quelle mesure $VT$ est différent de $E$, sachant que ces éléments des deux ensembles ne sont pas face-à-face. Il faut donc pouvoir « brancher » tous les éléments de $VT$ connectables avec les éléments de $E$ au regard des distances de Levenstein et mesurer des pertes dans le transport de $VT$ vers $E$.
Remarques en vrac sur la matrice de similarité
Avant de résoudre le problème que l’on vient de poser, on peut faire des remarques sur la nature de la matrice de similarité.
Tout d’abord sa complexité, qui est celle d’un produit cartésien entre le nombre d’éléments de $VT$ et d’éléments de $E$.
On remarque aussi que la matrice semble symétrique (la distance entre $VT _i$ et $E_i$ est la même que de $E_i$ à $VT _i$); qu’il n’y a pas de nombres négatifs; et qu’une distance nulle revient à dire qu’un élément dans $VT$ est égale à un élément dans $E$; que toutes les distances sont finies. Ce sont en fait des propriétés topologiques triviales qui nous permettent de croire que l’on manipule un espace métrique ! Cependant, l’inégalité triangulaire, requise pour prétendre avoir un espace métrique, n’est pas nécessairement vérifiée, étant donné que nous n’avons pas une matrice carrée (on a deux ensembles différents). A ce stade, notre matrice de similarité n’est donc pas une métrique à proprement parler… même si la distance de Levenshtein l’est. C’est davantage un plan de comparaison.
Le transport optimal
Une très brève présentation
Pour cette partie, je m’appuie sur des conférences et articles de Gabriel Peyré, directeur de recherche au CNRS, et plus spécialement celui-ci.
C’est ici que le problème de Monge intervient. Monge s’est demandé s’il était possible de calculer la façon la plus économique de transporter des tas de sables vers des trous à remblayer. Chaque tas de sable est à telle ou telle distance de chaque trou. Les valeurs du tableau expriment le temps en minutes qu’une brouette met pour atteindre un trou:
| Trou 1 | Trou 2 | Trou 3 | |
|---|---|---|---|
| Brouette 1 | 5 | 8 | 4 |
| Brouette 2 | 6 | 7 | 9 |
| Brouette 3 | 3 | 6 | 5 |
La brouette n°1 est à 5 minutes du trou n°1, à 8 du trou 2, à 4 minutes du trou 3; la brouette 2 à 6 minutes du trou 1, etc. On se demande quel trou faut-il attribuer quelle brouette pour minimiser le « coût temporel » des transports. La configuration la plus économique — celle qui prend le moins de temps — est donc la plus petite somme possible des temps du trajet réalisé par chaque brouette. Ici la solution est 14 : 4 minutes (brouette 1 -> trou 3) + 7 minutes (brouette 2 -> trou 2) + 3 minutes (brouette 3 -> trou 1). Elle diffère de la solution « gloutone », qui aurait proposé la solution 4 + 6 + 6 = 16 minutes.
Monge n’a pas pu résoudre le problème de façon générale. Il a en revanche posé des éléments permettant de le formaliser. De façon empirique, on peut calculer le coût de chaque configuration possible et prendre la meilleure. En sachant que tester toutes les configurations revient à tester $n!$ possibilités — puisqu’il s’agit de choisir la meilleure permutation — ce qui est énorme en terme de calcul. Par exemple, pour seulement 10 trous et autant de brouettes on a $10! = 3628800$ configurations à calculer et à comparer. Pour $20!$ on a $2 432 902 008 176 640 000$ permutations, ce qui est impossible à mettre en œuvre, et plus encore si nos données contiennent plus de dix éléments — et c’est en général bien le cas.
Voici la formalisation du problème par Monge pour trois brouettes et trois trous : $\min_{\sigma \in \Sigma_3} \text{Coût}(\sigma)$, sachant que le coût est défini ainsi : $\text{Coût}(\sigma) = C_{1,\sigma(1)} + C_{2,\sigma(2)} + C_{3,\sigma(3)}$ et $\sigma$ comme une coordonnée $i, j$ du tableau montré plus haut (la valeur d’une cellule).
C’est Leonid Kantorovich, en 1942, qui a trouvé la solution à ce problème de transport en représentant le problème différemment. Pour l’expliquer rapidement, il a d’abord exprimé l’ensemble des matrices de permutations de façon plus « compacte » en utilisant une somme double pour parcourir toutes les possibilités et en « filtrant » seulement les éléments matchés avec une matrice binaire, qui multiplie la matrice de coût, qui représente les permutations (un seul « 1 » pour chaque ligne et pour chaque colonne, le reste étant des zéros). Cela permet déjà de ne pas trouver les permutations à la main, d’exprimer tout d’un coup. Puis, il a « relaxé » la contrainte en remplaçant les matrices binaires par des matrices bistochastiques (des matrices pouvant admettre des valeurs entre 0 et 1) — il s’agit sommairement de matrices de probabilités où, cette fois, c’est la somme de chaque ligne et colonne qui doit faire 1. Il résulte de cette approche une plus grande souplesse et une plus grande généralité en considérant le problème non plus de façon combinatoire mais probabiliste. On passe donc d’un espace discret à un espace continu. (Ce qui ne veut pas dire non plus que le « probabilisme » de Kantorovitch implique de considérer des éléments comme des fruits du hasard mais plutôt comme des masses distribuées le long des lignes et des colonnes.) A titre illustratif, voilà à quoi ressemble la formulation de Kantorovitch pour résoudre des cas discrets. Du reste, je ne détaille pas davantage, les exemples qui suivent plus bas seront plus parlants:
$$\min_{P \in B_n} \sum_{i=1}^n \sum_{j=1}^n P_{i,j} C_{i,j}$$
Je ne passe pas plus de temps sur l’explication de la formulation Kantorivtch, mais je vous invite à lire l‘excellent article de vulgarisation de Gabriel Peyré.
Si vous vous demandez à quoi servent les énormes lettres grecques (sigma), je vous renvoie vers un de mes billets de blog sur la somme de Gauss. (Il n’y a vraiment rien de sorcier.)
Comparer la vérité terrain avec des données générées : est-ce un problème de transport optimal ?
Ce problème est celui l’évaluation de la sortie structurée par rapport à une vérité terrain. C’est une affaire de comparaison et ainsi on veut savoir « combien » la sortie structurée diffère de la vérité terrain. Le transport optimal trouve le meilleur « match global » entre les objets générés et les objets de référence, en tenant compte de leur similarité individuelle et de leur distribution globale en regardant la permutation qui minimise les distances. Avec cela, on peut calculer la somme des distances des seuls éléments appariés. Le transport optimal ne fait pas tout — n’offre pas toute cuite une métrique sur laquelle établir des analyses — mais permet de savoir quoi brancher avec quoi sans tester toutes les permutations (en rappelant que sans cela, l’espace de recherche de la bonne permutation croît selon une complexité factorielle). A noter également que l’optimisation peut trouver des paires « justifiées » mais pas forcément justes car elle ne tient pas compte de l’ordre. L’approche n’est peut-être pas la plus pertinente étant donné la nature séquentielle des données (et du reste il faudra par la suite peut-être adopter une approche moins synchronique ou appliquer une contrainte ordinale sur les appairages).
Cette approche pourrait être particulièrement pertinente en archivistique pour l’alignement d’instruments de recherche, considérant un ensemble A d’inventaires écrits par des personnes différentes; et un ensemble B des balises autorisées.
Il faut aussi garder en tête que c’est une méthode numérique et la notion d’optimisation ne coïncide pas forcément avec des notions plus subtiles, de nature sémantique. Sur une distance de Levenshtein, on ne peut pas apparier « sénateur » avec « parlementaire » (et on pourrait utiliser des embeddings pour aller plus loin mais ce n’est pas mon propos ici !). Mais dans mon cas la température du LLM est paramétrée à zéro ce qui, semble-t-il, l’empêche de traduire de façon « créative » les mots et se contente de rapporter des mots qu’il a trouvé, en cassant quelques hyphénations.
L’implémentation du transport optimal en Python
Il existe déjà une fonction, de la librairie Scipy, qui permet d’obtenir la meilleure permutation, linear_sum_assignment, mais sans les matrices bistochastiques. Elle permet donc d’obtenir les appairages les moins coûteux; appairage de type one-to-one car on emploie pas le fractionnement de masse qui « floute » les attributions possibles — utiles cependant si on veut faire des matchs one-to-many. C’est donc une implémentation technique du problème de transport optimal selon Kantorovitch, mais dans le cas discret (grosso-modo des ensembles dénombrables) et fini.

A noter que le résultat de cette fonction donne les appairages les plus optimaux : c’est donc bien une permutation qui a été choisie; nous avons pas de métrique. Sans aller plus loin, je mentionne la distance de Wasserstein qui permet d’obtenir une métrique à partir des éléments appariés et de leurs distances.
Cas concret : appairage entre $VT$ et $E$
Voici mon code qui emploie linear_sum_assignment (text_values_1 et text_values_2 contiennent respectivement les nœuds textuels de $VT$ et de $E$):
text_values1 = all_values[0]
text_values2 = all_values[1]
# uilise linear_sum_assignment pour trouver les appariements optimaux
row_ind, col_ind = linear_sum_assignment(similarity_matrix)
matched_in_text_values1 = set(row_ind)
# dico pour les appariements pour un accès rapide
match_dict = {i: j for i, j in zip(row_ind, col_ind)}
# affiche les résultats dans l'ordre ordinal de text_values1
for i, value in enumerate(text_values1):
if i in matched_in_text_values1:
# si l'élément est apparié, afficher l'appariement
j = match_dict[i]
print(f'"{value}" -----(score : {similarity_matrix[i, j]:.2f})-----> "{text_values2[j]}"')
else:
# Si l'élément n'est pas apparié, afficher sans correspondance
print(f'"{value}" -----(score : X)-----> <aucun match>')
# Afficher les éléments de text_values2 qui n'ont pas de correspondance
matched_in_text_values2 = set(col_ind)
for j, value in enumerate(text_values2):
if j not in matched_in_text_values2:
print(f'"aucun match" <-----(score : X)----- "{value}"')Ce qui me donne (extrait) :
"Babin-Chevaye" -----(distance : 0.00)-----> "Babin-Chevaye"
"8" -----(distance : 0.00)-----> "8"
"582" -----(distance : 0.00)-----> "582"
"719" -----(distance : 0.00)-----> "719"
"Bachelet (Alexandre)" -----(distance : 0.00)-----> "Bachelet (Alexandre)"
"V. Alexandre Bachelet" -----(distance : 3.00)-----> "Alexandre Bachelet"
"Barthou (Louis)" -----(distance : 0.00)-----> "Barthou (Louis)"
"2" -----(distance : 0.00)-----> "2"
"Barthou (Louis)" -----(distance : X)-----> <aucun match>
"394" -----(distance : 0.00)-----> "394"
"396" -----(distance : 0.00)-----> "396"
"397" -----(distance : 0.00)-----> "397"
"399" -----(distance : 0.00)-----> "399"
"1211" -----(distance : 0.00)-----> "1211"
"1237" -----(distance : 0.00)-----> "1237"
[...]
"Bérard (Victor)" -----(distance : X)-----> <aucun match>
"229" -----(distance : X)-----> <aucun match>
"233" -----(distance : 2.00)-----> "738"
"286" -----(distance : X)-----> <aucun match>
"579" -----(distance : X)-----> <aucun match>
"581" -----(distance : X)-----> <aucun match>
"628" -----(distance : X)-----> <aucun match>
"643" -----(distance : X)-----> <aucun match>On remarque que certains éléments on été loupés. Par exemple « Bérard (Victor) » qui pourtant est bien dans le texte brut issu de l’OCR :
Bérard (Victor). — Parle: discuss. d'un pro-
jet de loi concernant l'acte général d'arbi
trage, en qualité de président de la com-
mission des affaires étrangères, p. 229. —
= disouss. d'un projet de loi portant appr
bation du traité de conciliation et d'arbitrage
obligatoire conclu entre le Portugal et la
France, en qualité de président de la com-
mission, p. 233. — = discuss. d'une pro-
position relative à la licence ès lettres, p.
286.… mais pas dans le JSON. On a détecté ici une omission. Cela peut être du au fait qu’il y ait un « Bérard Louis » qui ait induit en erreur.
Le cas de la deuxième occurence de « Barthou Louis », qui n’a pas été trouvé, est aussi intéressant. Dans le texte de l’OCR, ces deux occurrences sont bien présentes:
Barthou (Louis), ministre de la guerre.
Son allocution à l'occasion du décès du ma-
réchal Joffre, p. 2.
Barthou (Louis). — Parle: disouss. d'un pro-
jet de loi relatif à l'exploitation des lignes de
laéropostale, p. 394, 396, 397, 399. — SOn
amendement déposé au cours de la diseuss.
d'un projet de loi portant ouverture et annu-
lation de crédits sur lexercice 1930-1931 a
titre du budget général et des budgets an-
nexes, p. 1211. — Parle: rectification au pro-
cès-verbal, p. 1237.Il est mentionné deux fois car il est intervenu en qualité de sénateur et de ministre.

En revanche, le LLM n’a pas répété deux fois son nom et a agrégé toutes les informations relatives à cet intervenant (je rappelle que je ne teste pour l’instant que les références de pages):
{
"nom": "Barthou (Louis)",
"references_pages": [
2,
394,
396,
397,
399,
1211,
1237
]
}Voici la vérité terrain :
{
"nom": "Barthou (Louis)",
"references_pages": [
2
]
},
{
"nom": "Barthou (Louis)",
"references_pages": [
394,
396,
397,
399,
1211,
1237
]
}On peut d’ailleurs discuter de l’autorité de la vérité terrain qui est davantage du « design » (la notion d’objectivité en théorie du design apportant d’ailleurs du grain à la réflexion3) : « La diversité d[u traitement des données] comme de leur rendu est fonction également du type de données produites et des conventions de représentation. Celles-ci dépendent de la succession des médiations techniques dont elles font l’objet dans leur traitement, elles sont elles-mêmes dépendantes des instruments utilisés. » (Anne-Lyse Renon, p. 115). Dans certains cas en effet, comme lorsqu’il y a « agrégation » de données normalement dispersées dans plusieurs entrées, avons-nous affaire à une erreur ? Ici, la répétition peut être signifiante (indique qu’un intervenant a eu une fonction) mais on peut aussi imaginer une version de la vérité terrain qui admet une telle agrégation. En tout cas il faut avoir en tête que je ne présente ici qu’une version « épurée », avec pages et noms, pour expérimenter autour de la problématique d’évaluation.
A ce stade, il y a déjà beaucoup de questions qui se posent : quel modèle génératif utiliser car est-ce que les loupés dépendent du modèle ? Quel « design » du modèle de données utiliser ? Le prompt est-il suffisamment robuste ? Peut-on générer de façon itérative le meilleur prompt possible grâce à la vérité terrain et, à partir de là commencer une évaluation ? On peut voir ce qui a été oublié; mais peut-on détecter ce qui a été halluciné ? Et surtout, quelle métrique utiliser pour donner des clés de compréhension globale à ces objections ?
Le « mètre » ignorant
On l’a vu, la matrice de similarité ne permet pas de conclure car ce n’est pas une métrique. Les résultats de l’assignement ne sont pas une métrique non plus (ou en tout cas autant que le sable est du verre).
La question est de savoir quelle métrique utiliser pour quantifier le transport (les bonnes assignations) de $VT$ à $E$. De plus, il faut aussi regarder si la structure elle-même, en JSON, est bien « transportée »; se demander s’il faut s’appuyer sur les ensembles des distances de Levenshtein des éléments appariés pour évaluer les structures. Il y a encore beaucoup de choses en suspens que je laisse pour un prochain article, cette fois sur l’assignement des structures JSON entre-elles et la métrique à utiliser.
- Cédric Villani, « Transport optimal de mesure : coup de neuf pour un très vieux problème », Images des mathématiques, 2004, pp. 114-119. ↩︎
- Gabriel Peyré, « Le transport optimal » (vidéo) : https://youtu.be/vQOF-3Hp6bY?si=bpaV_lL9zoGTnclE ↩︎
- Anne-Lyse Renon, Design & sciences, Saint-Denis, Presses universitaires de Vincennes, 2020, 196 pages ↩︎
EDIT : autre article intéressant :
Laisser un commentaire