Dans le billet précédent, j’ai établi les problématiques de l’évaluation de la sortie structurée pour des tâches de type indexation. Mais beaucoup de questions restaient en suspens, à commencer par l’analyse au niveau de la structure des objets et la métrique à utiliser. Dans cette partie — la dernière ? — il s’agira donc d’exposer des résultats avec des métriques « classiques » et deux autres, issues et adaptée du travail de deux chercheurs à l’EPITA, qui établissent la qualité des appariements.
Je remercie Joseph et Marie pour leurs retours.
EDIT (10 juillet): Après vérification IMQ et IRQ ne sont pas deux métriques différentes. Elles sont équivalentes : il ne faut donc pas prendre en compte la métrique de concordance.
Mesurer pour savoir, savoir ce qu’il faut mesurer (et mesurer ce que l’on tient à savoir)
Il est question ici de continuer sur les aspects techniques de ce qui a été amorcé la dernière fois autour de cette problématique : comment justifier en SHS un usage scientifique des données générées par un LLM ? Autrement dit, quoi et comment mesurer les données qu’il a produites pour telle question de recherche ? Cette problématique mériterait sans doute un article à part entière et on ne fera que l’aborder en filigrane. Il est cependant honnête d’en dispenser un fond de sauce ici, même brièvement, pour ne pas servir cru les résultats obtenus. On va tenter de prendre au sérieux l’idée de mesure car elle concerne aussi bien des résultats quantitatifs que les pratiques qui les font émerger.
Valuation, évaluation
En histoire, par exemple, on pourrait employer les modèles génératifs (comme Chat GPT ou Mistral) pour extraire les entités nommées d’archives numérisées. Avec ces données, on pourrait constituer des bases de données dans un format standard afin de répondre avec une question de recherche ou à des besoins prosopographiques. Ici, on s’intéresse à la dimension technique de l’évaluation de ces LLMs afin de savoir dans quelle mesure ses résultats sont exploitables. Derrière des enjeux très pragmatiques de l’utilisation de données pour un besoin contingent, il y a le décor aux allures épistémologiques de la « valuation ». La valuation est ce qui justifie le choix a priori de telles méthodes pour enquêter sur les données « en-vue-de ».
La valuation est un terme que j’emploie en pensant au philosophe pragmatiste John Dewey : la valuation prépare l’évaluation. Tout dispositif de savoir implique des choix de design, souvent tacites : formats, métriques, seuils, ontologies, visualisations… Et que ces choix ne sont pas neutres, mais porteurs de modèles du monde.
L’exploitabilité des données peut être exprimée par des métriques qui indiquent combien on peut donner créance au travail du LLM. Le choix des métriques n’est pas un absolu objectif car tout dépend de ce qu’on veut analyser, de ce à quoi on tient à savoir. Il y a alors une sorte de diplomatie entre des besoins concrets exigés par une question de recherche « SHS » et de la traduction technique des valuations qui déterminent les moyens d’évaluation appropriés. En somme, pour faire parler l’ami philosophique Gaston Bachelard, « les instruments sont de la théorie réifiée ». On a besoin de mesurer pour savoir si des données sont exploitables; mais il faut aussi savoir ce qu’il faudrait mesurer par rapport à ce que l’on désire savoir (et comment). Il y a là une sorte de co-détermination de la prémisse et de la conclusion — ou des moyens et des fins — qu’il ne faudrait malgré tout ne pas confondre avec une contradiction logique indépassable, laquelle empêcherait toute installation de prétentions scientifiques. C’est justement sachant cela — et sans jamais dire que tout se vaudrait parce qu’il n’y a effectivement pas de faits sans valeurs — qu’il faut entrer dans une démarche de rectification, démarche d’ailleurs parfaitement participante aux critères de scientificité.
La question prépare la mesure
Cela étant dit, il faut se mettre maintenant à la place de l’historien.ne, travaillé par une question de recherche ou cherchant à en formuler une : je veux avoir un aperçu (voire une cartographie) de l’activité parlementaire des sénateurs pour l’année 1931. (Car je veux avoir par exemple une photographie d’une période critique.) Je veux savoir qui parle et quand (et on pourrait imaginer de quoi). Sachant que le Journal Officiel restitue l’activité parlementaire et que le Journal Officiel a une pagination annuelle continue (la page 1 correspond au premier jour d’activité de l’année qui tombe en janvier, et la dernière page à la dernière séance, en décembre), il m’importe donc de collecter l’ensemble des activités datées (ou « datables ») de chaque intervenant au sénat (sénateurs, mais aussi ministres interpellés). Les tables du Sénat m’offrent une telle liste, mais sans les dates — qui sont donc supposées avec la pagination. Pour ce faire, je veux extraire automatiquement des données issues des tables du Sénat (disponibles sur Gallica). Mais, comme on s’imagine en historien sérieux, je veux être sûr que ces données soient vraies — ou suffisamment fiables pour en dire quelque chose avec prudence — car je les exploite pour ma thèse. Ma valeur de référence ce sont bien les entrées car chacune d’elle représente un acteur de l’activité de la Chambre Haute.

Ce que l’on tient à savoir : les entrées générées par le LLM contiennent-elles des données bien structurées et « solidaires » ? (Par exemple, on veut être sûr que telle page concerne bien tel sénateur afin de ne pas lui attribuer une activité qui ne lui appartient pas.) De « combien » dévient-elles par rapport à une vérité terrain ? peut-on ainsi faire confiance aux données générées ?
Traduction quantitative des besoins énoncés
Autrement dit, en faisant un parallèle avec les exemples classiques de la statistique, on cherche à évaluer un système de traitement selon les critères suivants :
- Sa précision : les données générées sont-elles fiables ?
(« Y a-t-il eu un bon diagnostic ? »)
→ Puis-je légitimement me fier aux données produites, en considérant un « taux de justesse » parmi les appariements réalisés ? - Son rappel : est-ce que les données produites couvrent l’ensemble des cas ou seulement une partie ?
(« A-t-on diagnostiqué tous les patients ou seulement certains ? »)
→ Puis-je dire que les résultats sont globalement représentatifs de l’ensemble des cas à traiter ? - Son F-score : une moyenne harmonique entre précision et rappel qui combine ces deux dimensions.
(« La méthodologie de diagnostic est-elle globalement satisfaisante ? »)
→ Un compromis entre justesse et couverture.
On veut appliquer ces idées au niveau des entrées qu’on a appariés. D’après le travail de chercheurs à l’EPITA1, il est utile de proposer une métrique sur la qualité des appariements en eux-mêmes, car ces scores s’y basent:
- La qualité moyenne des appariements (AMQ pour average matching quality) qui mesure la fidélité des appariements individuels (par exemple via une distance de similarité). « (Les appariements sont-ils chacun de bonne qualité, même si leur nombre est limité ?)«
- La qualité globale des appariements (OMQ pour overall matching quality) qui tient compte à la fois de la qualité des appariements et de leur couverture. (« En combinant justesse et exhaustivité, à quel point peut-on dire que l’ensemble du travail est fiable ? »)

On peut aller encore plus loin pour estimer les limitations inhérentes à la méthode d’appariement choisie qui peut fragiliser la légitimité des scores, à savoir ici le transport optimal. C’est une méthode qui a été choisie parmi d’autres possibles. Car en effet, on pourrait imaginer d’autres méthodes d’appariements. Par exemple, étant donné que les données se suivent, avec un algorithme glouton : il choisirait, pour chaque vérité terrain, et dans l’ordre où cela vient, la donnée prédite avec la distance de Levenshtein la plus faible. Mais à mesure que l’on avance dans les appariements, on prive potentiellement les derniers des appariements qui pourrait leur être dû.
Et… on pourrait aller encore plus loin en déterminant si la notion de distance, sur laquelle se base des appariements et le score sur le qualité des appariements est la plus judicieuse possible en étudiant la « métricité » des matrices de coût (leur « topologie »). Ici, c’est une hypothèse personnelle très spéculative, assez peu utile en pratique mais que je trouve intéressante. Je la mentionnerai aussi plus bas juste pour le plaisir de la spéculation.
Dans le billet précédent, on a tout mis à plat : on a comparé chaque nœud textuel et fait des appariements sans se soucier du rapport hiérarchique entre les données. Cela a permis d’exposer « à plat » la notion de distance (notamment de Levenshtein) et celle de transport optimal. Mais notre véritable valeur, ce sont les entrées et tout ce qu’elles encapsulent. Ces entrées, ce sont donc les objets JSON :
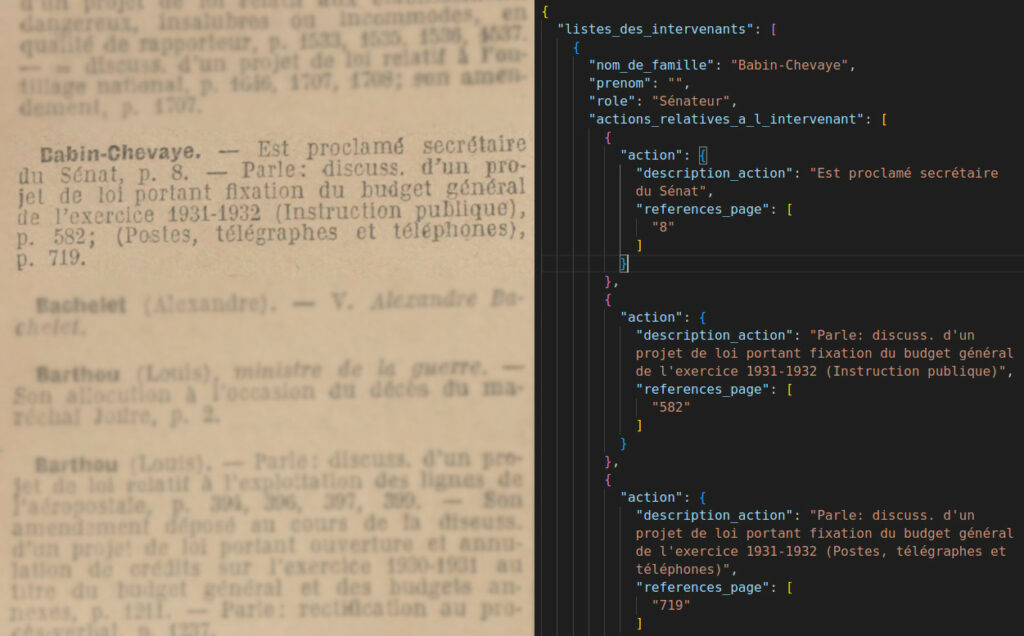
Comme mentionné la dernière fois, le transport optimal n’est pas vraiment une méthode « diachronique » elle peut apparier des éléments très loin pour peu que ça soit mathématiquement justifié (« peu couteux »). En comparant avec une matrice de similarité et en appariant à plat les éléments les plus proches on peut fragiliser la dimension hiérarchique du JSON.
De fait, sur mes données de test, ça n’est pas arrivé : mais rien n’indique, étant donné la nature « permutative » du transport optimal, qu’on ait un jour localement une mauvaise combine, même si ça assure un bon match global. C’est une approche solide et qui peut-être appliquée à d’autres corpus avec des mises en page plus exotique, moins linéaires.
Comme on veut garder la solidarité des entrées pour les évaluer, c’est donc elles qu’il faut comparer en vue d’apparier, et même si une des informations, côté données générées par le LLM, est manquant ou faux car on veut justement en évaluer la précision.

A noter : on aurait aussi très bien pu utiliser une moyenne des distances des éléments appariés à plat en redécoupant par dessus avec une Regex puisque nos entrées commencent par des lettres et finissent pas un nombre. On aurait pu réengager le travail de la dernière fois. De fait, c’est une approche risquée (car on ne sait pas a priori à quoi peuvent ressembler nos données) et absolument pas applicables à l’échelle. Comme on le voit déjà, il y a plusieurs façons de faire, et elles ont leurs raisons selon moi. Je crois cependant que l’heuristique de la manipulation directe d’entrée « as objects » est plus expressive. C’est un meilleur « design » sachant notre question de recherche.
Mise en pratique : implémenter les métriques en Python
Pour cette partie, je remercie bien sûr Joseph de m’avoir proposé un script à partir duquel j’ai pu broder des classes et comprendre toutes les métriques !
Passage à la POO (programmation orientée objet)
On va réadapter ce qu’on a fait la dernière fois en POO. Traduit en Python, on peut représenter chaque entrée (donc chaque acteur) comme l’instance d’une classe Entry dans laquelle on injectera les éléments du JSON:
class Entry:
def __init__(self, data: RawEntry):
"""Initialization with data from json (object)"""
self.data = data
def get(self) -> RawEntry:
"""Return the entire object"""
return self.dataOn pourra utiliser cette classe aussi bien pour la vérité terrain que pour les données prédites. Cette classe représente donc les données qui vont être comparées. On peut lui ajouter une méthode qui permet d’afficher ce qu’elle contient (.get()).
On aura aussi une seconde classe dédiée à la comparaison de ces entrées, la classe `Matcher`:
class Matcher:
def __init__(self, entries_a: List[Entry], entries_b: List[Entry], distance_method: str = "ratcliff"):
"""A Matcher is a comparator; he compares two sets of entry and produces a matrix"""
self.entries_a = entries_a
self.entries_b = entries_b
self.distance_method = distance_method
self.cost_matrix = self.compute_cost_matrix(distance_method)
self.matches = self.match()Elle prend donc comme paramètre une entrée A (la vérité terrain par exemple) et une entrée B (les données générées); et également un paramètre pour choisir la distance sur laquelle se basera la matrice de coût. Je n’ai pas encore, à ce stade, fait de paramètre pour choisir la méthode d’appariement, n’utilisant que le transport optimal pour l’instant.
On va maintenant implémenter ce qu’on a vu la dernière fois, à commencer par la matrice de coût qui est une prérogative du Matcher. On ajoute cette méthode à la classe Matcher :
#Méthode de la classe Matcher
def compute_cost_matrix(self, distance_method: str = "ratcliff") -> np.ndarray:
n, m = len(self.entries_a), len(self.entries_b)
cost_matrix = np.zeros((n, m))
for i, entry_a in enumerate(self.entries_a):
for j, entry_b in enumerate(self.entries_b):
if distance_method == "levenshtein":
cost_matrix[i, j] = entry_a.distance_to_levenshtein(entry_b)
else:
cost_matrix[i, j] = entry_a.distance_to(entry_b)
return cost_matrixIci, on peut choisir d’utiliser soit la distance de Levensthein — soit celle de Ratcliff/Obershelp. Cette option peut être utile si on veut faire une CLI à partir du script.
Pour le reste de l’article, j’utiliserai la distance de Ratcliff/Obershelp car elle produit par défaut des résultats normalisés (entre 0 et 1) et elle gère mieux les inversions (par exemple
Larcher (Gérard)etGérard Larcher)
J’ai fait ici le choix de retourner les distances depuis une méthode « distance_to » de ‘Entry‘. C’est un choix discutable, mais l’idée est que chaque entrée « sache » à quelle distance elle peut se trouver d’un autre entrée. Et c’est Matcher qui peut la demander :
# Méthode de la classe Entry
def distance_to(self, other: 'Entry') -> float:
"""Return distance between him and an another object"""
"""NB : ==> average field-to-field distances (Ratcliff/Obershelp)"""
def field_distance(f1: str, f2: str) -> float:
return 1 - SequenceMatcher(None, f1, f2).ratio()
total = 0.0
count = 0
# Compare fields with the same label
for field in ["nom", "references_pages"]:
norm_self = self.normalize_field(field)
norm_other = other.normalize_field(field)
if norm_self or norm_other:
total += field_distance(norm_self, norm_other)
count += 1
return total / count if count else 1.0On va maintenant implémenter le travail d’appariement qui, pour le coup, revient de droit au Matcher :
# Méthode de Matcher
def match(self) -> List[Tuple[int, int]]:
"""A faire : paramètre pour choisir la méthode d'assignement"""
row_ind, col_ind = linear_sum_assignment(self.cost_matrix)
return list(zip(row_ind, col_ind))Il n’y a ici qu’une seule façon d’apparier. Mais, dans l’optique de développement d’une CLI, on pourrait imaginer une option qui permet de choisir d’autres algorithmes d’appairage.
💻 Retrouvez le code complet sur mon repository Github : https://github.com/desireesdata/Evaluate-Structured-Output
⚠️ Notez que c’est un travail en cours. Tout ce qui concerne les métriques sont des méthodes de la classe Matcher, dans matcher.py
Sans détailler plus, on peut générer un tableau des appariements avec l’information des distances (et donc des qualités, valant $1-\text{distance}$) :
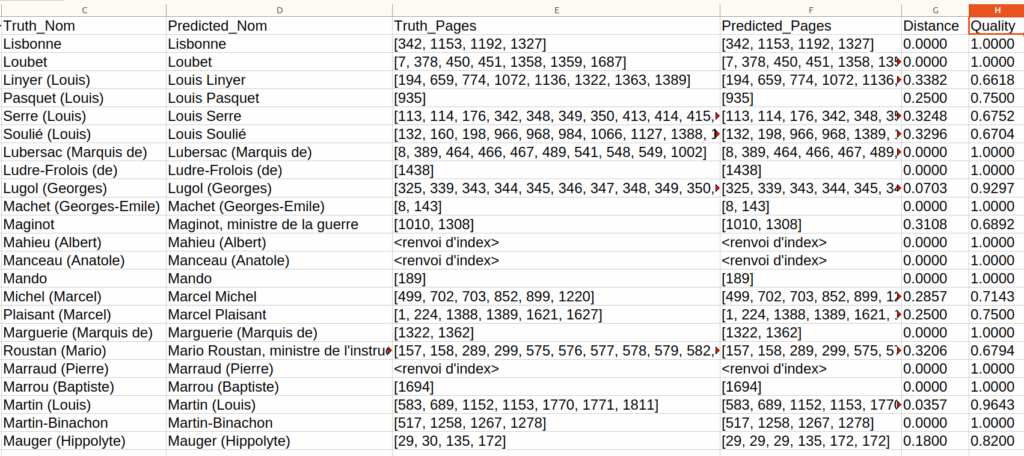
Des statistiques « opaques » : précision, rappel, F1
Maintenant que l’on peut sortir des appariements, il ne reste plus qu’à les évaluer ! Ici, on va calculer la précision (« les données générées sont elles fidèles ? »), le rappel (« a-t-on toutes les données ? » et le F-score (F1, « un score qui combine précision et rappel »). C’est encore une prérogative du Matcher :
# Méthode de MAtcher
def compute_precision_recall_f1(self) -> Dict[str, float]:
tp = len(self.matches)
fp = len(self.entries_b) - tp
fn = len(self.entries_a) - tp
precision = tp / (tp + fp) if (tp + fp) else 0.0
recall = tp / (tp + fn) if (tp + fn) else 0.0
f1 = 2 * precision * recall / (precision + recall) if (precision + recall) else 0.0
return {"Precision": precision, "Recall": recall, "F1": f1}C’est ici qu’il faut prendre un peu de temps. La précision, le rappel et le F1 reposent sur le calcul de trois valeurs : $TP, FP, FN$ (True Positive, False Positive, False Negative):
- $TP$ représente le nombre d’appariements trouvés;
- $FP$ représente nombre total de prédictions moins le nombre de vrais positifs. Cela représente les prédictions qui ne correspondent à aucune entrée de la vérité terrain;
- $FN$ représente le nombre total d’entrées de la vérité terrain moins le nombre de vrais positifs (de matchs). Cela représente les entrées de la vérité terrain qui n’ont pas été correctement prédites.
On le voit : ces valeurs reposent sur la cardinalité (le nombre total) de différents ensembles. Cela veut dire qu’on ne regarde pas la « qualité » des appariements, juste leur quantité. Cela a ses limites car on pourrait très bien avoir des doublons et des éléments manqués qui se compensent quantitativement. Ainsi, la fonction Python compute_precision_recal_f1 dit :
- “J’ai
len(self.matches)appariements que je considère comme vrais positifs ($TP$).” - Puis elle suppose que tout ce qui n’est pas apparié est un faux négatif (FN) ou un faux positif (FP).
… Et pour terminer, elle applique ensuite les formules classiques de précision / rappel / F1 que je ne détaille pas ici puisque le code Python est assez explicite.

Premiers résultats « opaques » de la sortie structurée (et premiers biais)
Dans mon cas, j’ai testé la sortie structurée à partir de cinq pages OCRisés de trois manières différentes :
- OCR corrigé à main, réputé sans fautes (un OCR « parfait »);
- OCR obtenu via un outil de zoning manuel développé par le projet Mezanno (« Corpusense », en développement);
- OCR plus « brut », via Corpusense également, qui couvre toute la page, sans se soucier des zones d’intérêts (couvre par exemple le foliotage)
Il y a en tout 108 entrées (et donc 324 lignes). Voici les résultats (sur une échelle de 0 à 1):
Source | Precision | Recall | F1 | Nombre d’entrées vérité terrain |
|---|---|---|---|---|
| page 02 ZONES | 1.0000 | 0.9130 | 0.9545 | 23 |
| page 02 OCR PARFAIT | 1.0000 | 1.0000 | 1.0000 | 23 |
| page 02 OCR BRUT | 1.0000 | 0.9565 | 0.9778 | 23 |
| page 03 OCR BRUT | 1.0000 | 1.0000 | 1.0000 | 25 |
| page 03 ZONES | 1.0000 | 1.0000 | 1.0000 | 25 |
| page 03 OCR PARFAIT | 1.0000 | 1.0000 | 1.0000 | 25 |
| page 04 OCR BRUT | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 04 OCR PARFAIT | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 04 OCR ZONES | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 05 OCR PARFAIT | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 05 OCR ZONES | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 05 OCR BRUT | 1.0000 | 1.0000 | 1.0000 | 19 |
| page 10 ZONES | 1.0000 | 1.0000 | 1.0000 | 23 |
| page 10 BRUT | 1.0000 | 1.0000 | 1.0000 | 23 |
| page 10 OCR PARFAIT | 1.0000 | 1.0000 | 1.0000 | 23 |
On a donc, semble-t-il, de bons résultats. Trop bons ?
A) Précision
La précision à 100% voudrait dire — notez le conditionnel — que tous les appariements sont bons. De fait, j’insiste, on a pas vraiment regardé la qualité des appariements, on a juste regardé si chaque élément a été apparié… ce qui est forcément le cas étant donné que le transport optimal fait du one-to-one. Elle ne dit rien de pertinent puisqu’on a considéré tous les appariements comme des $TP$, true positive. On pourrait alors vouloir écrire de nouvelles vérités terrains représentant les bons appariements et coder un script pour vérifier si c’est bien le cas (chronophage) ou considérer que la précision ici n’est pas pertinente sachant que l’on a deux métriques pour la qualité des appariements, mentionnées plus haut. Cependant, rien n’empêche de jeter un œil aux appariements faits et de constater qu’effectivement, en tout cas du côté des noms, toutes les entrées sont bien trouvées même si, évidemment, l’orthographe varie (parenthèses absentes, noms écrits en majuscules…). Mais cette remarque n’a rien de très solide, méthodologiquement parlant.
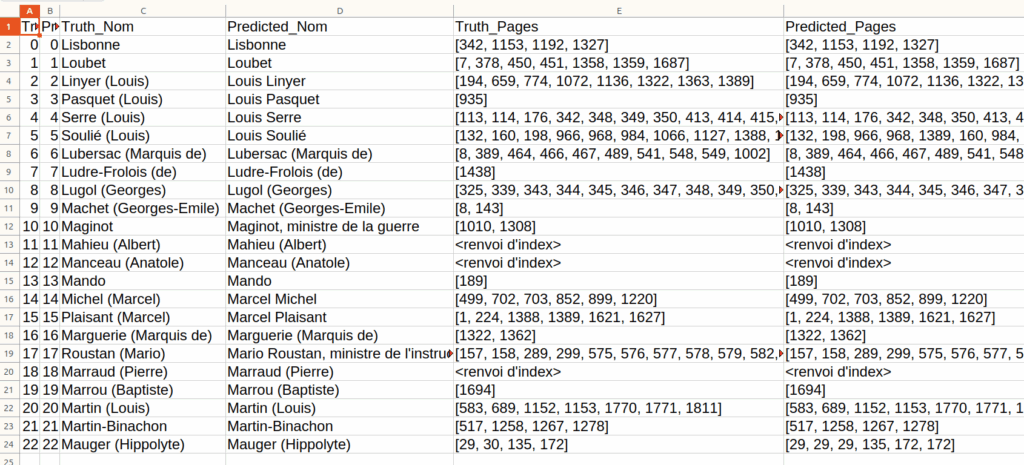
B) Rappel
Du côté du rappel (recall), on a de bons résultats, mais qui ne tapent pas à 100%. Cela veut dire qu’on a pas oublié d’entrées, sauf pour la page deux. Regardons un fragment de la vérité terrain et ce qu’elle représente :
{
"nom": "Barthou (Louis), ministre de la guerre",
"references_pages": [
2
]
},
{
"nom": "Barthou (Louis)",
"references_pages": [
394,
396,
397,
399,
1211,
1237
]
},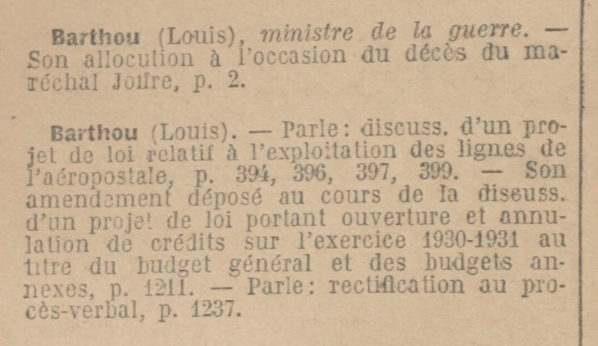
On le voit, il y a une affaire de choix dans la vérité terrain. J’ai choisi de faire deux entrées pour Barthou Louis mais on aurait très bien pu faire une seule entrée et tout factoriser car, après tout, il s’agit bien d’établir une liste des interventions par personne au Sénat. J’ai fait le choix de reproduire cette répétition car on ne peut pas démontrer a priori que dans l’ensemble de mes données — et la vérité terrain n’est qu’un échantillon — il y ait pas un jour des homonymes — et donc qu’il faut bien prendre en compte les séparations entre les entrées. Ne sachant pas a priori à quoi peuvent ressembler mes données, s’il y aura des homonymes ou non, je préfère donc répéter. Ici, bien sûr, cette répétition est signifiante, elle n’est pas celle d’une homonymie. Elle indique que notre sénateur a aussi joué un rôle de ministre de la guerre.
Côté sorties structurées prédites, on trouve quelque chose comme ça :
{
"nom": "Barthou (Louis)",
"references_pages": [
2,
394,
396,
397,
399,
1211,
1237
]
},Le LLM a donc choisi de factoriser et c’est la raison que le recall n’est pas à 100% car ce genre de répétition n’a pas été pris en compte.
Seulement il y a un problème. Concernant le score très haut du recall en général (99% en moyenne), cela voudrait dire que le LLM ne loupe pas d’entrées — le 1% étant le fait du design de la vérité terrain. Cet excellent score d’exhaustivité n’est en fait pas pleinement signifiant: cela tient en fait à la nature du transport optimal qui « force » un appariement.
C) Biais
On a donc là aussi, pour le rappel comme le score de précision, un biais évident. (Même si, d’une certaine façon, le rappel est moins biaisé que la précision.) Car ici, on ne fait que regarder si tous nos cas sont traités. Cela gonfle forcément le résultat car on ne laisse aucun cas de la vérité terrain sans traitement.
Et ne parlons pas du F1 doublement biaisé puisqu’il se base sur le recall et la précision. Ces métriques classiques ne sont pas, en l’état, adaptées à notre cas du fait de la nature injective du transport optimal… à défaut de vouloir multiplier les vérités terrain. Il faut prendre en considération la qualité des appariements.
Casser l’opacité : une affaire de surfaces (IMQ, IRQ)
On a donc un problème : précision et rappel ne sont pas des indicateurs fiables car on a opté pour un appariement one-to-one, forcé par le transport optimal — même si le recall est moins biaisé que la précision. (Ce qui ne veut pas dire que le transport optimal est une mauvaise solution. D’ailleurs, en jetant un œil aux données, il semble bien qu’on aurait un score très proche de 100%.) On pourrait tenir à savoir malgré tout la précision et le recall pour avoir un F-score. Mais la démarche de créer encore des vérités terrains est une démarche lourde et on peut exiger dans notre cahier des charges de réduire « l’intervention humaine » dans le processus et de se cantonner à vérifier la sortie structurée, non pas toute la logique d’appariement, etc.
On pourrait alors, puisqu’on a des appariements et les distances qui leur sont attachées, ne compter que ceux qui sont au-delà d’un seuil, par exemple $0.70$.
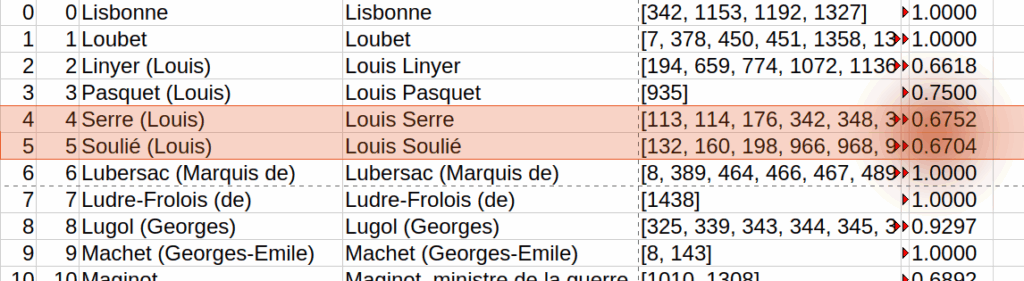
Mais quel seuil choisir raisonnablement ? On voit qu’on a aussi de bons matchs qui sont sous ce seuil; mais on ne veut pas non plus tolérer des choses qui ne sont pas des bons appariements. Est-il raisonnable de choisir arbitrairement ce seuil ?

On peut imaginer une solution, inspirée de la logique des courbes d’AUC et du COCO Panoptic, qui mise sur le calcul de l’aire de la courbe sous différents seuils de tolérance. On dispose de la distance de chaque paire effective et on calcule une « qualité » qui vaut $1 – distance$. Au lieu de tout accepter comme des $TP$ comme le fait actuellement notre score de précision, on se demande comment calculer le bon seuil: « Plus la qualité demandée est haute, plus je suis strict. Quelle proportion de mes appariements ‘survivent’ à cette exigence qui augment petit à petit ? ». On prend donc tous les seuils : en intégrant (et normalisant) ce balayage de l’ensemble des seuils, on calcule un score qui, s’il tend vers 1, montre la bonne robustesse des matchs; et s’il tend vers 0; des matches fragiles. Essayons donc de formaliser le calcul de l’aire dessinée par balayage de l’ensemble de seuils de tolérance :
$F(t)$ est la fonction de couverture par seuil de qualité : elle donne, pour chaque seuil $t \in [0, 1]$, la proportion de matches ayant une qualité au moins égale à $t$ :
$$
F(t) = \frac{1}{n} \sum_{k=1}^{n} {1}_{{q_k \geq t}}
$$
On veut donc calculer l’aire sous cette courbe — appelons cette métrique Integrated Matching quality (IMQ) — on fait référence aux deux dernières métriques que nous allons voir juste après même si l’IMQ n’a rien d’original:
$$\text{IMQ} = \int_{0}^{1} F(t) dt$$
En voici l’implémentation (étant donné qu’on discrétise l’intégrale, on utilise des « pas », la granularité de 1000 est arbitraire):
def compute_integrated_matching_quality(self, steps: int = 1000) -> float:
if not self.matches:
return 0.0
qualities = np.array([1.0 - self.cost_matrix[i, j] for i, j in self.matches])
thresholds = np.linspace(0, 1, steps)
area = 0.0
for t in thresholds:
coverage = np.sum(qualities >= t) / len(self.entries_a)
area += coverage
return area / stepsL’IMQ est une sorte de « précisionoïde » : elle est la métrique qui se substitue (tant bien que mal) à la précision étant donné la nature de notre appariement.
Pour avoir maintenant un ersatz de rappel, on peut proposer la métrique de l’ « IRQ » (Integrated Recall Quality). Le rappel compte la proportion d’éléments trouvés par rapport au nombre total d’éléments trouvables. Notre IRQ va compter de façon floue en prenant en compte les poids (la qualité) de chaque appariement et compter 0 pour les données de la vérité terrain qui n’ont pas été appariés (pour « punir » les oublis). C’est en fait une bête moyenne des qualités :
$$\text{IRQ} = \frac{1}{n} \sum_{i=1}^{n} \left(1_{\text{apparié}}(i) \cdot q_i \right)$$
Ce qui donne en Python :
def compute_irq(self) -> float:
if not self.matches:
return 0.0
matched_dict = {i: j for i, j in self.matches}
total_quality = 0.0
for i in range(len(self.entries_a)):
if i in matched_dict:
j = matched_dict[i]
total_quality += 1.0 - self.cost_matrix[i, j]
else:
total_quality += 0.0
return total_quality / len(self.entries_a)Maintenant que l’on a un rappeloïde et un précisionoïde, on peut faire notre « F-scoroïde » (F1Q, pour « quality »), utilisant ces deux métriques pour avoir une mesure de performance conjointe (moyenne-harmonique-core) :
$$\text{F1Q} = \frac{2 \cdot \text{IMQ} \cdot \text{IRQ}}{\text{IMQ} + \text{IRQ}}$$
Ce qui donne en Python :
def compute_f1q(self) -> float:
imq = self.compute_integrated_matching_quality()
irq = self.compute_irq()
if imq + irq == 0:
return 0.0
return 2 * (imq * irq) / (imq + irq)Ces métriques ne sont pas des rustines : elles offrent au contraire une information qualitative sur les appariements. Comment les interpréter ? Eh bien, elles déplacent le regard : on ne demande plus seulement « combien d’éléments sont correctement détectés ? », mais « avec quelle qualité sont-ils détectés ? » malgré (ou sachant) le « forcing » du transport optimal :
- L’IMQ mesure la robustesse globale des appariements retenus, quel que soit leur nombre : elle indique si ceux qui ont été appariés l’ont été avec une bonne similarité. Elle ignore donc les oublis (faux négatifs) et se concentre sur la fiabilité des appariements effectivement établis.
- l’IRQ, au contraire, ne pardonne pas les absences : elle prend en compte chaque élément de la vérité terrain, attribuant une qualité s’il est apparié, ou un zéro sinon. Elle joue le rôle d’un rappel flou, et fournit une vue populationnelle du succès de l’appariement, incluant les cas silencieux.
- l’F1Q les combine dans une perspective équilibrée. C’est un compromis harmonique entre la qualité des appariements réalisés (IMQ) et leur couverture (IRQ). Il est donc particulièrement utile comme score synthétique, car il chute dès que l’une des deux composantes faiblit.
Nous voilà finalement pas si mal lotis : ces trois métriques permettent d’aller au-delà du comptage binaire des TP/FP/FN, pour évaluer la qualité réelle du matching.
Sur la convergence entre IMQ et IRQ (… et donc F1Q)
Une observation intéressante émerge : lorsqu’on applique ces métriques à un système d’appariement comme le mien : l’IMQ (précisionoïde) et l’IRQ (rappeloïde) peuvent parfois afficher des valeurs quasi-identiques, avec un écart absolu négligeable (de quelques centièmes). Cela ne signifie pas que l’une est redondante. Mais plutôt que le système évalue des appariements à la fois nombreux et de bonne qualité, et cela sans omettre de correspondances significatives.
Pour le dire autrement, le transport optimal agit déjà comme un filtre robuste — ce qui tend à faire converger les deux scores. On peut imaginer que, dans des situations moins idéales (transport « pas optimal », vérité terrain incomplète, matches partiels), IRQ et IMQ se désaligneront naturellement. L’intérêt de conserver les deux permet de bien distinguer la couverture floue (IRQ) de la précision floue (IMQ). Ainsi, la convergence des deux scores est une démonstration que l’appariement est bien… optimal.
Et la boucle est bouclée : nous pouvons démontrer a posteriori que le transport optimal, qui est pourtant le domaine a priori des appariements, est une bonne approche quand $IMQ$ est (presque) égal à $IRQ$. La convergence d’IMQ et IRQ démontre un bon appariement.
Cela veut dire que la formule générale de notre $FQ1$ est celle de $IMQ$ ou de $IRQ$. On a donc trois métriques (presque) identiques mais qu’il est utile de garder pour démontrer que l’appariement est légitime. On pourrait alors esquisser une métrique de concordance entre ces deux valeurs :
$$
\text{Concordance} = 1 – |\text{IMQ} – \text{IRQ}|
$$
Cette métrique n’étant pas assez sensible, on peut la cuisiner de cette façon pour faire apparaître de façon expressive les défauts ($\epsilon$ vaut 0.001) :
$$\text{Concordance Expressive} = 1 – \frac{|\text{IMQ} – \text{IRQ}|}{(\text{IMQ} + \text{IRQ}) / 2 + \epsilon}$$
Pour résumer : la convergence (IMQ ≈ IRQ) indique qu’il n’y a pas de compromis entre la « précision » des appariements (IMQ) et leur « couverture » (IRQ). Le système n’est pas seulement bon pour ce qu’il trouve, il trouve aussi la quasi-totalité de ce qu’il devrait, et ce, avec une qualité similaire. C’est une validation forte que le transport optimal n’abuse pas et fait des appariements de qualité.
Une autre métrique taillée pour le transport optimal, la distance de Wasserstein
Avant de passer sur les dernières métriques, je me dois de mentionner quelque chose d’important. Je ne fais, encore une fois, que mentionner cette distance, celle de Wasserstein, qui pourrait, modulo du bricolage, constituer une métrique. Il y a vraiment une carte à jouer ici étant donné la nature de nos appariements. J’ai fait des tests mais rien de très expressif pour l’instant. Mais cette idée mériterait d’être approfondie ultérieurement.
De la transparence : évaluer les appariements avec l’AMQ et l’OMQ
En s’appuyant sur l’article cité précédemment (COCO Panoptic), outre les métriques IMQ/IRQ/F1Q, on peut vouloir résumer la qualité des appariements par des scores plus compacts, orientés vers une lecture globale du système. C’est le rôle des métriques AMQ, OMQ, et OMQ (IMQ-based) :
- AMQ (Average Matching Quality) : c’est la moyenne brute des qualités des appariements réalisés. Contrairement à IMQ, elle ne les pondère pas selon des seuils ni ne tient compte de leur distribution. C’est un indicateur direct de la fidélité moyenne des correspondances établies.
- OMQ (Overall Matching Quality) introduit une combinaison tripartite : elle intègre la précision, le rappel, et la qualité moyenne des matches (AMQ) dans une moyenne harmonique à trois dimensions. Son objectif est de fournir une mesure de performance globale, tenant compte à la fois de la quantité et de la qualité de l’appariement. Un système performant est donc attendu d’avoir une OMQ élevée, signalant qu’il appaire bien, suffisamment, et proprement.
- OMQ basée sur l’IMQ: reprend la même idée que l’OMQ, mais en remplaçant la précision par l’IMQ, pour mieux refléter les cas où la frontière entre bons et mauvais appariements est floue. Cette variante généralise donc l’OMQ en adoptant une lecture plus tolérante mais plus fine de ce qu’est une bonne correspondance.
Mais comment ? On utilise toujours le rappel alors qu’on a dit que c’était un paramètre biaisé ? Eh bien on a justement démontré avec la convergence de IMQ et IRQ que nos appariements étaient bons. Cela suggère que les appariements sélectionnés par le transport optimal sont non seulement pertinents, mais aussi homogènes en qualité — en témoigne aussi la valeur de convergence expressive. Dans un tel cadre, le rappel peut être réhabilité comme un indicateur « raisonnable » (donc pas parfait) de la couverture effective, et servir de facteur multiplicatif pour des métriques comme l’OMQ.
On pourrait aussi calculer la variance des qualités pour vérifier l’homogénéité des qualités… mais point trop n’en faut.
Ces scores condensés — AMQ pour la qualité brute, OMQ pour l’équilibre complet, et OMQ (IMQ-based) pour la lecture plus souple — permettent de résumer des systèmes complexes en une valeur synthétique, tout en gardant une sensibilité à la richesse de l’information portée par la qualité d’appariement.
Voici l’implémentation Python :
def compute_overall_matching_quality_imq(self) -> float:
"""
Version de l'OMQ (Overall Matching Quality) basée sur l'IMQ (Integrated Matching Quality),
qui remplace la précision pour tenir compte de la qualité de tous les appariements.
"""
imq = self.compute_integrated_matching_quality()
recall = self.compute_precision_recall_f1()["Recall"]
avg_quality = self.compute_average_matching_quality()
denom = (imq * recall + imq * avg_quality + recall * avg_quality)
if denom == 0:
return 0.0
return 3 * (imq * recall * avg_quality) / denom
def compute_average_matching_quality(self) -> float:
"""AMQ"""
if not self.matches:
return 0.0
total_quality = sum(1. - self.cost_matrix[i, j] for i, j in self.matches)
return total_quality / len(self.matches)
def compute_overall_matching_quality(self) -> float:
"""OMQ"""
metrics = self.compute_precision_recall_f1()
avg_quality = self.compute_average_matching_quality()
precision = metrics["Precision"]
recall = metrics["Recall"]
denom = (precision * recall + precision * avg_quality + recall * avg_quality)
if denom == 0:
return 0.0
return 3 * (precision * recall * avg_quality) / denom
Résultats & limites
Aperçu des résultats
Maintenant que nous avons des métriques qui conviennent à nos données et à notre méthode d’appariement, les résultats.
J’ai effectué le traitement pour les 5 pages et leurs 3 variantes (OCR parfait, OCR via l’outil Corpusense et OCR brut) de façon séparée (avec des entrées coupées). J’ai donc 15 salves de résulats. Mais pour plus de lisibilité et ne pas surcharger cet article déjà bien long, je vais discuter de la moyenne des résultats. Il faudra me croire : cette moyenne est un bon représentant.
| Metric | Value |
|---|---|
| Precision | 1.000000 |
| Recall | 0.991300 |
| F1 | 0.995487 |
| Integrated Matching Quality (IMQ) « présionoïde » | 0.908000 |
| Integrated Recall Quality (IRQ) « rappeloïde » | 0.908120 |
| F1Q (« F-scoroïde ») | 0.908040 |
| Concordance expressive | 0.999868 |
| Average Matching Quality (AMQ) | 0.916640 |
| Overall Matching Quality (OMQ) | 0.966793 |
| Overall Matching Quality (IMQ-based) | 0.936247 |
Les résultats agrégés sur les cinq pages analysées témoignent d’un bon comportement du système d’appariement, bien que les métriques classiques ne puissent à elles seules en rendre compte de façon fiable. En effet, dans notre cadre basé sur un appariement par transport optimal, les scores de précision, rappel et F1 tendent à être trompeurs. La précision brute affichée à 1.0 suggère qu’aucun faux positif n’a été généré, tandis qu’un rappel de 0.991 indique que presque toutes les entrées de la vérité terrain ont été associées à une prédiction. Mais cette lecture, on le rappelle, est biaisée : l’appariement impose des contraintes structurelles (notamment l’unicité des correspondances), ce qui rend ces indicateurs partiellement aveugles à la finesse réelle des associations effectuées.
C’est précisément pour cette raison que nous avons introduit des métriques adaptées à la nature de notre tâche. L’Integrated Matching Quality (IMQ) et l’Integrated Recall Quality (IRQ), conçues comme des analogues flous de la précision et du rappel, s’établissent toutes deux autour de 0.908, signalant une grande cohérence dans la qualité des appariements. Quant à la très faible différence entre IMQ et IRQ, elle révèle non seulement un équilibre entre couverture et pertinence, mais aussi une très bonne homogénéité des appariements. Cette stabilité est encore renforcée par le score de concordance expressive, qui frôle la perfection (0.9999) : il mesure à quel point l’IMQ et l’IRQ convergent, et donc à quel point le système ne sacrifie ni la qualité, ni la couverture.
Enfin, les autres métriques viennent compléter cette analyse qualitative. L’Average Matching Quality (AMQ) à 0.916 indique que les correspondances sélectionnées sont localement très bonnes. Les scores d’Overall Matching Quality — classiques (0.967) et basés sur l’IMQ (0.936) — traduisent la performance globale du système en tenant compte à la fois du volume et de la qualité des appariements. Ces mesures renforcent l’idée que l’algorithme est capable de retrouver les bons éléments même dans des conditions imparfaites (entrées tronquées, ambiguïtés), et qu’il le fait avec une finesse appréciable. Les limites résident surtout dans la difficulté à traiter certains cas très ambigus ou lacunaires, mais les scores montrent que de telles situations restent marginales.
Les données de la sortie structurées sont-elles exploitables ? Plutôt oui. Mais il est essentiel d’en exposer les limites de façon explicite.
Aperçu des limites
Si les 100% ne sont pas atteints, c’est parce que le texte sur lequel de base la sortie structurée n’est pas parfait : en effet les marges « attaquent » les capacités du modèle d’OCR :

Il y a également le contexte textuel, tronqué : je n’ai pas vraiment traité des pages se suivant, puisque j’ai séparé volontairement la générations de données pour avoir un scénario pessimiste. Car il est plus facile pour un LLM — ici Ministral 8b — d’avoir un contexte complet que fragmenté. Si bien que, parfois, l’information issue d’une entrée tronquée au début d’une page est distribuée sur les suivantes.
Il arrive aussi que certains numéros de page (en général avec quatre chiffres), pourtant présents dans le texte OCRisé sont tous simplement ignorés. Je pense que le LLM doit les confondre avec des dates.
Les intervenants ayant eu deux fonctions, comme on l’a vu, change le nombre d’entrées et font baisser la qualité du rappeloïde.
Il y a des erreurs typographiques dans le document d’origine. Par exemple des points à la place de virgules. Ce qui peut troubler le LLM dans la détection des pages. Des tâches sur le papier peuvent aussi déconcentrer le LLM et/ou le moteur d’OCR (et ainsi mélanger l’ordre des lignes):

Le prompt pourrait être amélioré — et il faudrait pouvoir faire des diagnostics sur la qualité du prompt. Mais chaque nouvelle variable à tester multiplie les combinaisons de paramètres à prendre en compte. Pour une prochaine fois ?
La structure de la vérité terrain, elle-même, pourrait être amendée.
La structure des données, également. Il semble bien que « commenter » les champs avec Field(...) offre de meilleurs résultats. Il serait aussi intéressant de quantifier la nature ou le contenu de ces champs. Ici, encore, on multiplie les pipelines à évaluer.
class Intervenant(BaseModel):
nom: str = Field(..., description="Nom (et prénom s'il existe) de l'intervenant")
references_pages: Union[List[int], str] = Field(..., description="Liste des numéros de page où l'intervenant est référencé ou sinon <renvoi d'index>")
class IntervenantAuSenat(BaseModel):
listes_des_intervenants: List[Intervenant] = Field(..., description="Liste de tous les intervenants avec leurs références de pages respectives")Le modèle choisi n’est pas forcément le plus pertinent. En prenant un petit modèle peu spécialisé — et surtout à l’API facile d’accès et à utiliser — j’ai essayé de renforcer une situation « pessimiste ».
La distance choisie pour préparer l’appariement, forcément, biaise les résultats. J’ai finalement opté pour une distance de Ratcliff/Obershelp car elle offrait sur étagère une métrique normalisée et était pertinente par rapport aux jeux de permutations entre les noms et prénoms des sénateurs. Une distance de Levenshtein normalisée aurait pu faire l’affaire, mais forcément cela modifie la « qualité » des appariements et donc a posteriori des métriques.
Ici, j’ai notamment une piste pour répondre à la question : « comment motiver un choix de distance ? ». Des éléments de réponse en deux mots : on remarque que parmi les matrices de similarité, le seul cas qui a des propriétés métriques est un match parfait. On peut donc étudier la « métricité » d’une matrice de similarité imparfaite, bruitée, en relachant localement les propriétés métriques (symétrie, inégalité triangulaire et identité). Ce relâchement peut être quantifié et il traduit la distance d’une matrice imparfaite à une matrice parfaite. Ainsi, on pourrait diagnostiquer la « métricité » d’une matrice de similarité selon telle ou telle distance. Cela pourrait faire un article de blog intéressant !
Une brève conclusion
En tout cas on voit que les stratégies d’évaluation sont une sorte de cuisine de métriques. La nature des données à évaluer impliquent d’ajuster les métriques classiques pour répondre à des besoins particuliers. Elles dépendent également la nature de ce qu’on tient à savoir (car, on pourrait imaginer sanctionner plus durement les pages manquées si on cherche à établir une timeline fiable de l’activité parlementaire de 1931). La notion de métrique, dépendante de la valuation, dépeignent des états de faits, quantifiés, qui hurlent de valeurs.
Cela ne veut pas dire que la démarche quantitative est inconsistante vis à vis des critiques épistémologiques classiques — à la façon de Vilèm Flusser — qui ont tendance à renforcer malgré tout le dualisme fait/valeur, nombre/qualité, science/art, etc. Ici, j’ai pleine conscience que les résultats sont pétris par des valuations; mais qu’on a aussi besoin de motiver la cuisine des résultats justement pour que, dans une optique de transparence et d’ouverture des données, il n’y ait pas privatisation des chemins (des méthodes) qui peuvent mener à la connaissance — si modestes et laborieux soient-ils.
Coda
Des pistes après les résultats, en vrac : on peut utiliser les données produites pour entraîner un modèle plus léger (de type Bert); faire une visualisation de l’activité parlementaire en 1931; continuer l’évaluation et en particulier en prenant en considération le prompt.
- Joseph Chazalon, Edwin Carlinet, « Revisiting the Coco Panoptic Metric to Enable Visual and Qualitative Analysis of Historical Map Instance Segmentation » ↩︎
Répondre à La topologie appliquée aux données documentaires et patrimoniales : petit topo récréatif sur l’évaluation de la sortie structurée via LLMs – désirées data Annuler la réponse